mirror of
https://github.com/mfocko/blog.git
synced 2025-05-04 10:22:58 +02:00
blog(leetcode): add matrix sort
Signed-off-by: Matej Focko <mfocko@redhat.com>
This commit is contained in:
parent
d6644d74ab
commit
7ed3cd3298
3 changed files with 919 additions and 0 deletions
blog/leetcode
static/files/blog/leetcode/sort-matrix-diagonally
674
blog/leetcode/sort-matrix-diagonally.md
Normal file
674
blog/leetcode/sort-matrix-diagonally.md
Normal file
|
|
@ -0,0 +1,674 @@
|
||||||
|
---
|
||||||
|
title: Sort the matrix diagonally
|
||||||
|
description: Compiler assisted development.
|
||||||
|
date: 2023-03-04T23:15
|
||||||
|
slug: leetcode/sort-diagonally
|
||||||
|
authors:
|
||||||
|
- name: Matej Focko
|
||||||
|
title: "a.k.a. @mf"
|
||||||
|
url: https://gitlab.com/mfocko
|
||||||
|
image_url: https://github.com/mfocko.png
|
||||||
|
tags:
|
||||||
|
- cpp
|
||||||
|
- leetcode
|
||||||
|
- iterators
|
||||||
|
hide_table_of_contents: false
|
||||||
|
---
|
||||||
|
|
||||||
|
Let's try to solve one of the LeetCode challenges in easy and hard mode at the
|
||||||
|
same time.
|
||||||
|
|
||||||
|
<!--truncate-->
|
||||||
|
|
||||||
|
* Link to the problem: https://leetcode.com/problems/sort-the-matrix-diagonally/
|
||||||
|
|
||||||
|
## Problem description
|
||||||
|
|
||||||
|
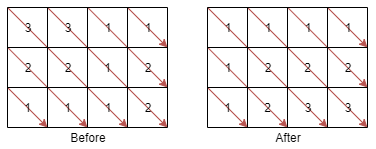
A **matrix diagonal** is a diagonal line of cells starting from some cell in
|
||||||
|
either the topmost row or leftmost column and going in the bottom-right direction
|
||||||
|
until reaching the matrix's end. For example, the **matrix diagonal** starting
|
||||||
|
from `mat[2][0]`, where `mat` is a `6 x 3` matrix, includes cells `mat[2][0]`,
|
||||||
|
`mat[3][1]`, and `mat[4][2]`.
|
||||||
|
|
||||||
|
Given an `m x n` matrix `mat` of integers, sort each matrix diagonal in ascending
|
||||||
|
order and return the resulting matrix.
|
||||||
|
|
||||||
|
### Example
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
## Skeleton and initial adjustments
|
||||||
|
|
||||||
|
We are given the following skeleton for the C++ and the given challenge:
|
||||||
|
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
vector<vector<int>> diagonalSort(vector<vector<int>>& mat) {
|
||||||
|
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|
||||||
|
The task is to sort the passed matrix diagonally and then return it. First of all,
|
||||||
|
I don't like to solve this in a web browser, so we'll need to adjust it accordingly
|
||||||
|
for running it locally. We'll start by including the `vector` header and using
|
||||||
|
fully-qualified namespaces[^1] and also adding few tests:
|
||||||
|
|
||||||
|
```cpp
|
||||||
|
#include <cassert>
|
||||||
|
#include <vector>
|
||||||
|
|
||||||
|
using matrix = std::vector<std::vector<int>>;
|
||||||
|
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
matrix diagonalSort(matrix& mat)
|
||||||
|
{
|
||||||
|
}
|
||||||
|
};
|
||||||
|
|
||||||
|
static void test_case_1()
|
||||||
|
{
|
||||||
|
// Input: mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
|
||||||
|
// Output: [[1,1,1,1],[1,2,2,2],[1,2,3,3]]
|
||||||
|
|
||||||
|
Solution s;
|
||||||
|
assert((s.diagonalSort(std::vector { std::vector { 3, 3, 1, 1 },
|
||||||
|
std::vector { 2, 2, 1, 2 },
|
||||||
|
std::vector { 1, 1, 1, 2 } })
|
||||||
|
== std::vector { std::vector { 1, 1, 1, 1 },
|
||||||
|
std::vector { 1, 2, 2, 2 },
|
||||||
|
std::vector { 1, 2, 3, 3 } }));
|
||||||
|
}
|
||||||
|
|
||||||
|
static void test_case_2()
|
||||||
|
{
|
||||||
|
// Input: mat =
|
||||||
|
// [[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]]
|
||||||
|
// Output:
|
||||||
|
// [[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]
|
||||||
|
|
||||||
|
Solution s;
|
||||||
|
assert((s.diagonalSort(std::vector { std::vector { 11, 25, 66, 1, 69, 7 },
|
||||||
|
std::vector { 23, 55, 17, 45, 15, 52 },
|
||||||
|
std::vector { 75, 31, 36, 44, 58, 8 },
|
||||||
|
std::vector { 22, 27, 33, 25, 68, 4 },
|
||||||
|
std::vector { 84, 28, 14, 11, 5, 50 } })
|
||||||
|
== std::vector { std::vector { 5, 17, 4, 1, 52, 7 },
|
||||||
|
std::vector { 11, 11, 25, 45, 8, 69 },
|
||||||
|
std::vector { 14, 23, 25, 44, 58, 15 },
|
||||||
|
std::vector { 22, 27, 31, 36, 50, 66 },
|
||||||
|
std::vector { 84, 28, 75, 33, 55, 68 } }));
|
||||||
|
}
|
||||||
|
|
||||||
|
int main()
|
||||||
|
{
|
||||||
|
test_case_1();
|
||||||
|
test_case_2();
|
||||||
|
|
||||||
|
return 0;
|
||||||
|
}
|
||||||
|
```
|
||||||
|
|
||||||
|
We need to return the matrix, but we're given a reference to the input matrix. We
|
||||||
|
can easily abuse the C++ here and just switch the reference to value, this way
|
||||||
|
the matrix will be copied when passed to the function, we can sort the copy and
|
||||||
|
just return it back. And we also get yelled by the compiler for the fact that the
|
||||||
|
method doesn't return anything yet, so to make it “shut up” we will just return
|
||||||
|
the input for now:
|
||||||
|
|
||||||
|
```diff
|
||||||
|
- matrix diagonalSort(matrix& mat)
|
||||||
|
+ matrix diagonalSort(matrix mat)
|
||||||
|
{
|
||||||
|
+ return mat;
|
||||||
|
}
|
||||||
|
```
|
||||||
|
|
||||||
|
Now, we get the copy and we're good to go.
|
||||||
|
|
||||||
|
## Naïve solution
|
||||||
|
|
||||||
|
As you may know, C++ offers a plethora of functions that can be used to your
|
||||||
|
advantage, given that you know how to “bend” the data structures accordingly.
|
||||||
|
|
||||||
|
What does that mean for us? Well, we have an `std::sort`, we can use it, right?
|
||||||
|
Let's have a look at it:
|
||||||
|
```cpp
|
||||||
|
template< class RandomIt >
|
||||||
|
void sort( RandomIt first, RandomIt last );
|
||||||
|
```
|
||||||
|
|
||||||
|
This overload is more than we need. What does it do? It just sorts the elements
|
||||||
|
in the range `[first, last)` using `operator<` on them. We can't sort the whole
|
||||||
|
matrix using this, but… we can sort just »one« diagonal without doing much work
|
||||||
|
on our end.
|
||||||
|
|
||||||
|
What is the `RandomIt` type though? If we look more into the documentation, we
|
||||||
|
can easily find the requirements for it and also learn that it's a _random access_
|
||||||
|
_iterator_ and allows swapping its values at the same time.
|
||||||
|
|
||||||
|
:::tip Random access iterator
|
||||||
|
|
||||||
|
What is the _random access iterator_ though? We can find it in a documentation
|
||||||
|
and see the following description:
|
||||||
|
|
||||||
|
> A **LegacyRandomAccessIterator** is a [LegacyBidirectionalIterator](https://en.cppreference.com/w/cpp/named_req/BidirectionalIterator)
|
||||||
|
> that can be moved to point to any element in constant time.
|
||||||
|
|
||||||
|
After that we can see all the requirements for it being listed. I don't feel like
|
||||||
|
reading them right now, so we will just use it and see where the compilation blows
|
||||||
|
up, i.e. “_compiler-assisted development_”[^2] if you will ;)
|
||||||
|
|
||||||
|
:::
|
||||||
|
|
||||||
|
Now we know that we can use `std::sort` to sort the diagonal itself, but we also
|
||||||
|
need to get the diagonals somehow. I'm rather lazy, so I'll just delegate it to
|
||||||
|
someone else[^3]. And that way we get
|
||||||
|
```cpp
|
||||||
|
matrix diagonalSort(matrix mat)
|
||||||
|
{
|
||||||
|
// we iterate over the diagonals
|
||||||
|
for (auto d : diagonals(mat)) {
|
||||||
|
// and we sort each diagonal
|
||||||
|
std::sort(d.begin(), d.end());
|
||||||
|
}
|
||||||
|
|
||||||
|
// we take the matrix by copy, so we can sort in-situ and return the copy
|
||||||
|
// that we sorted
|
||||||
|
return mat;
|
||||||
|
}
|
||||||
|
```
|
||||||
|
|
||||||
|
This solution looks very simple, doesn't it? Well, cause it is.
|
||||||
|
Let's try compiling it:
|
||||||
|
```
|
||||||
|
matrix-sort.cpp:11:23: error: use of undeclared identifier 'diagonals' [clang-diagnostic-error]
|
||||||
|
for (auto d : diagonals(mat)) {
|
||||||
|
^
|
||||||
|
Found compiler error(s).
|
||||||
|
make: *** [makefile:14: tidy] Error 1
|
||||||
|
```
|
||||||
|
|
||||||
|
OK, seems about right. We haven't implemented the `diagonals` yet. And based on
|
||||||
|
what we've written so far, we need a function or a class `diagonals` that will
|
||||||
|
give us the diagonals we need.
|
||||||
|
|
||||||
|
## Implementing the `diagonals`
|
||||||
|
|
||||||
|
Cool, so we need the function that will let us go through each and every diagonal
|
||||||
|
in our matrix. We use the _for-range_ loop, so whatever we get back from the
|
||||||
|
`diagonals` must support `.begin()` and `.end()`. Since I am a masochist, we will
|
||||||
|
do such functionality for a matrix of any type, not just the `int` from the challenge.
|
||||||
|
|
||||||
|
As I said, we need to be able to
|
||||||
|
* construct the object
|
||||||
|
* get the beginning
|
||||||
|
* get the end (the “sentinel”)
|
||||||
|
|
||||||
|
```cpp
|
||||||
|
template <typename T>
|
||||||
|
class diagonals {
|
||||||
|
using matrix_t = std::vector<std::vector<T>>;
|
||||||
|
|
||||||
|
matrix_t& _matrix;
|
||||||
|
|
||||||
|
public:
|
||||||
|
diagonals(matrix_t& m)
|
||||||
|
: _matrix(m)
|
||||||
|
{
|
||||||
|
}
|
||||||
|
diagonals_iter begin()
|
||||||
|
{
|
||||||
|
/* TODO */
|
||||||
|
}
|
||||||
|
diagonals_iter end()
|
||||||
|
{
|
||||||
|
/* TODO */
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|
||||||
|
Now we have a `diagonals` that we can use to go through the diagonals. We haven't
|
||||||
|
implemented the core of it yet. Let's go through what we have for now.
|
||||||
|
|
||||||
|
We have a templated class with templated `T` that is used as a placeholder for any
|
||||||
|
type we would store in the matrix. Because I'm lazy, I have defined the `matrix_t`
|
||||||
|
type that is a “shortcut” for `std::vector<std::vector<T>>`, so I don't have to
|
||||||
|
type it out all the time. Of course, we need to store the matrix, we are given,
|
||||||
|
as a private attribute. And then just have the constructor and the 2 methods we
|
||||||
|
need for the _for-range_.
|
||||||
|
|
||||||
|
### Iterating over diagonals
|
||||||
|
|
||||||
|
Now that we have an object that will allow us to iterate through the diagonals,
|
||||||
|
we need to implement the iterating itself. We need to go through all of them, so
|
||||||
|
we have multiple options how to do so. I have decided to start from the “main”
|
||||||
|
diagonal that starts at `(0, 0)` index and then proceed with the diagonals starting
|
||||||
|
in the first row, followed by the rest of the diagonals in the first column.
|
||||||
|
|
||||||
|
We need to be able to tell that we've iterated through all of them, and also we
|
||||||
|
need to know which diagonal is next. For that purpose we will pass the indices
|
||||||
|
of the first cell on the diagonal. That way we can always tell how to move forward.
|
||||||
|
|
||||||
|
We will start by updating the `begin` and `end` to reflect our choice accordingly.
|
||||||
|
|
||||||
|
```cpp
|
||||||
|
diagonals_iter begin() { return diagonals_iter { _matrix, 0, 0 }; }
|
||||||
|
diagonals_iter end() { return diagonals_iter { _matrix, 0, _matrix.size() }; }
|
||||||
|
```
|
||||||
|
|
||||||
|
For the `begin` we return the first diagonal that starts at `(0, 0)`. And because
|
||||||
|
we have decided to do the diagonals in the first column at the end, the first
|
||||||
|
diagonal that is not a valid one is the one at `(0, height)`. Apart from the
|
||||||
|
indices, we also need to pass reference to the matrix itself.
|
||||||
|
|
||||||
|
:::note
|
||||||
|
|
||||||
|
You may have noticed that we also include the diagonals that have length 1,
|
||||||
|
specifically the ones at `(0, height - 1)` and `(width - 1, 0)`. We are implementing
|
||||||
|
an iterator that **should not** care about the way it's being used. Therefore, we
|
||||||
|
don't care about the fact they don't need to be sorted.
|
||||||
|
|
||||||
|
:::
|
||||||
|
|
||||||
|
Cool, let's leave the iterator itself to someone else, right?[^4]
|
||||||
|
|
||||||
|
### Implementing the iterator over diagonals
|
||||||
|
|
||||||
|
We can start with a simple skeleton based on the information that we pass from
|
||||||
|
the `diagonals`. Also to utilize the `matrix_t` and also contain implementation
|
||||||
|
details hidden away, we will put this code into the `diagonals` class.
|
||||||
|
|
||||||
|
```cpp
|
||||||
|
class diagonals_iter {
|
||||||
|
matrix_t& m;
|
||||||
|
std::size_t x;
|
||||||
|
std::size_t y;
|
||||||
|
|
||||||
|
public:
|
||||||
|
diagonals_iter(matrix_t& matrix, std::size_t x, std::size_t y)
|
||||||
|
: m(matrix)
|
||||||
|
, x(x)
|
||||||
|
, y(y)
|
||||||
|
{
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|
||||||
|
In this case we will be implementing a “simple” forward iterator, so we don't
|
||||||
|
need to implement a lot. Notably it will be:
|
||||||
|
* inequality operator (we need to know when we reach the end and have nothing to
|
||||||
|
iterate over)
|
||||||
|
* preincrementation operator (we need to be able to move around the iterable)
|
||||||
|
* dereference operator (we need to be able to retrieve the objects we iterate
|
||||||
|
over)
|
||||||
|
|
||||||
|
```cpp
|
||||||
|
class diagonals_iter {
|
||||||
|
matrix_t& m;
|
||||||
|
std::size_t x;
|
||||||
|
std::size_t y;
|
||||||
|
|
||||||
|
public:
|
||||||
|
diagonals_iter(matrix_t& matrix, std::size_t x, std::size_t y)
|
||||||
|
: m(matrix)
|
||||||
|
, x(x)
|
||||||
|
, y(y)
|
||||||
|
{
|
||||||
|
}
|
||||||
|
|
||||||
|
bool operator!=(const diagonals_iter& rhs) const
|
||||||
|
{
|
||||||
|
// iterators are not equal if they reference different matrices, or
|
||||||
|
// their positions differ
|
||||||
|
return m != rhs.m || x != rhs.x || y != rhs.y;
|
||||||
|
}
|
||||||
|
|
||||||
|
diagonals_iter& operator++()
|
||||||
|
{
|
||||||
|
if (y != 0) {
|
||||||
|
// iterating through diagonals down the first column
|
||||||
|
y++;
|
||||||
|
return *this;
|
||||||
|
}
|
||||||
|
|
||||||
|
// iterating the diagonals along the first row
|
||||||
|
x++;
|
||||||
|
if (x == m.front().size()) {
|
||||||
|
// switching to diagonals in the first column
|
||||||
|
x = 0;
|
||||||
|
y++;
|
||||||
|
}
|
||||||
|
|
||||||
|
return *this;
|
||||||
|
}
|
||||||
|
|
||||||
|
diagonal<T> operator*() const { return diagonal { m, x, y }; }
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|
||||||
|
Let's go one-by-one. Inequality operator is rather simple, just compare iterator's
|
||||||
|
attributes field-by-field. If you think about it, checking inequality of two 2D
|
||||||
|
vectors may be a bit inefficient, therefore, we can swap around and check it as
|
||||||
|
a last thing.
|
||||||
|
|
||||||
|
```diff
|
||||||
|
- return m != rhs.m || x != rhs.x || y != rhs.y;
|
||||||
|
+ return x != rhs.x || y != rhs.y || m != rhs.m;
|
||||||
|
```
|
||||||
|
|
||||||
|
Preincrementation is where the magic happens. If you have a better look, you can
|
||||||
|
see two branches of this operation:
|
||||||
|
|
||||||
|
1. When `y != 0` (we're iterating over the diagonals in the first column)
|
||||||
|
In this case, we just bump the row and we're done.
|
||||||
|
2. When `y == 0` (we're iterating over the diagonals in the first row)
|
||||||
|
In this case, we bump the column and check if we haven't gotten out of bounds,
|
||||||
|
i.e. the end of the first row. If we get out of the bounds, we're continuing
|
||||||
|
with the second diagonal in the first column.
|
||||||
|
|
||||||
|
Dereferencing the iterator must “yield” something. In our case it will be the
|
||||||
|
diagonal that we want to sort. For sorting we need just the iterators that can
|
||||||
|
move around said diagonal. The simplest thing, we can do, is to delegate it to
|
||||||
|
something else. In our case it will be a class called `diagonal`.
|
||||||
|
|
||||||
|
## Implementing the `diagonal` itself
|
||||||
|
|
||||||
|
After implementing the iterator over diagonals, we know that all we need to describe
|
||||||
|
a diagonal is the matrix itself and the “start” of the diagonal (row and column).
|
||||||
|
And we also know that the diagonal must provide some iterators for the `std::sort`
|
||||||
|
function. We can start with the following skeleton:
|
||||||
|
```cpp
|
||||||
|
template <typename T>
|
||||||
|
class diagonal {
|
||||||
|
using matrix_t = std::vector<std::vector<T>>;
|
||||||
|
|
||||||
|
matrix_t& matrix;
|
||||||
|
std::size_t x;
|
||||||
|
std::size_t y;
|
||||||
|
|
||||||
|
public:
|
||||||
|
diagonal(matrix_t& matrix, std::size_t x, std::size_t y)
|
||||||
|
: matrix(matrix)
|
||||||
|
, x(x)
|
||||||
|
, y(y)
|
||||||
|
{
|
||||||
|
}
|
||||||
|
|
||||||
|
diagonal_iter begin() const { return diagonal_iter { matrix, x, y }; }
|
||||||
|
|
||||||
|
diagonal_iter end() const
|
||||||
|
{
|
||||||
|
auto max_x = matrix[y].size();
|
||||||
|
auto max_y = matrix.size();
|
||||||
|
|
||||||
|
// we need to find the distance in which we get out of bounds (either in
|
||||||
|
// column or row)
|
||||||
|
auto steps = std::min(max_x - x, max_y - y);
|
||||||
|
|
||||||
|
return diagonal_iter { matrix, x + steps, y + steps };
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|
||||||
|
Initialization is rather simple, we just “keep” the stuff we get, `begin` is the
|
||||||
|
simplest, we just delegate.
|
||||||
|
|
||||||
|
In case of the `end`, it gets more complicated. We need to know where is the “end”
|
||||||
|
of the diagonal. Since `end` should point to the first element “after” the iterable,
|
||||||
|
we know that it's the first position of the iterator where either `y` becomes
|
||||||
|
`matrix.size()` or `x` becomes `matrix[y].size()`. Also we are moving along diagonal,
|
||||||
|
duh, therefore we can deduce the first “position” afterwards by minimal amount of
|
||||||
|
steps to get out of the any column or row, hence `std::min(max_x - x, max_y - y)`.
|
||||||
|
Final position is then computed simply by adding the steps to the beginning of
|
||||||
|
the diagonal.
|
||||||
|
|
||||||
|
Now we just need to finish the iterator for the diagonal itself and we're done.
|
||||||
|
|
||||||
|
### Implementing `diagonal_iter`
|
||||||
|
|
||||||
|
This part is the hardest from all we need to do. It's because of the requirements
|
||||||
|
of the `std::sort` that requires us to implement a _random access iterator_. I have
|
||||||
|
briefly described it above, and “in a nutshell” it means that we need to implement
|
||||||
|
an iterator that can move in constant time along the diagonal in any amount of
|
||||||
|
steps.
|
||||||
|
|
||||||
|
Let's go through all of the functionality that our iterator needs to support to
|
||||||
|
be used in `std::sort`. We need the usual operations like:
|
||||||
|
|
||||||
|
* equality/inequality
|
||||||
|
* incrementation
|
||||||
|
* dereferencing
|
||||||
|
|
||||||
|
We will also add all the types that our iterator uses with the category of the
|
||||||
|
iterator, i.e. what interface it supports:
|
||||||
|
```cpp
|
||||||
|
class diagonal_iter {
|
||||||
|
// we need to keep reference to the matrix itself
|
||||||
|
matrix_t& m;
|
||||||
|
|
||||||
|
// we need to be able to tell our current position
|
||||||
|
std::size_t x;
|
||||||
|
std::size_t y;
|
||||||
|
|
||||||
|
public:
|
||||||
|
using difference_type = std::ptrdiff_t;
|
||||||
|
using value_type = T;
|
||||||
|
using pointer = T*;
|
||||||
|
using reference = T&;
|
||||||
|
using iterator_category = std::random_access_iterator_tag;
|
||||||
|
|
||||||
|
diagonal_iter(matrix_t& matrix,
|
||||||
|
std::size_t x,
|
||||||
|
std::size_t y)
|
||||||
|
: m(matrix)
|
||||||
|
, x(x)
|
||||||
|
, y(y)
|
||||||
|
{
|
||||||
|
}
|
||||||
|
|
||||||
|
bool operator==(const diagonal_iter& rhs) const
|
||||||
|
{
|
||||||
|
return x == rhs.x && y == rhs.y && m == rhs.m;
|
||||||
|
}
|
||||||
|
|
||||||
|
diagonal_iter& operator++()
|
||||||
|
{
|
||||||
|
// we are moving along the diagonal, so we increment both ‹x› and ‹y› at
|
||||||
|
// the same time
|
||||||
|
x++;
|
||||||
|
y++;
|
||||||
|
return *this;
|
||||||
|
}
|
||||||
|
|
||||||
|
reference operator*() const { return m[y][x]; }
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|
||||||
|
This is pretty similar to the previous iterator, but now we need to implement the
|
||||||
|
remaining requirements of the _random access iterator_. Let's see what those are:
|
||||||
|
|
||||||
|
* decrementation - cause we need to be able to move backwards too, since _random _
|
||||||
|
_access iterator_ extends the interface of _bidirectional iterator_
|
||||||
|
* moving the iterator in either direction by steps given as an integer
|
||||||
|
* being able to tell the distance between two iterators
|
||||||
|
* define an ordering on the iterators
|
||||||
|
|
||||||
|
Let's fill them in:
|
||||||
|
```cpp
|
||||||
|
class diagonal_iter {
|
||||||
|
// we need to keep reference to the matrix itself
|
||||||
|
matrix_t& m;
|
||||||
|
|
||||||
|
// we need to be able to tell our current position
|
||||||
|
std::size_t x;
|
||||||
|
std::size_t y;
|
||||||
|
|
||||||
|
public:
|
||||||
|
using difference_type = std::ptrdiff_t;
|
||||||
|
using value_type = T;
|
||||||
|
using pointer = T*;
|
||||||
|
using reference = T&;
|
||||||
|
using iterator_category = std::random_access_iterator_tag;
|
||||||
|
|
||||||
|
diagonal_iter(matrix_t& matrix,
|
||||||
|
std::size_t x,
|
||||||
|
std::size_t y)
|
||||||
|
: m(matrix)
|
||||||
|
, x(x)
|
||||||
|
, y(y)
|
||||||
|
{
|
||||||
|
}
|
||||||
|
|
||||||
|
bool operator==(const diagonal_iter& rhs) const
|
||||||
|
{
|
||||||
|
return x == rhs.x && y == rhs.y && m == rhs.m;
|
||||||
|
}
|
||||||
|
|
||||||
|
diagonal_iter& operator++()
|
||||||
|
{
|
||||||
|
// we are moving along the diagonal, so we increment both ‹x› and ‹y› at
|
||||||
|
// the same time
|
||||||
|
x++;
|
||||||
|
y++;
|
||||||
|
return *this;
|
||||||
|
}
|
||||||
|
|
||||||
|
reference operator*() const { return m[y][x]; }
|
||||||
|
|
||||||
|
// exactly opposite to the incrementation
|
||||||
|
diagonal_iter operator--()
|
||||||
|
{
|
||||||
|
x--;
|
||||||
|
y--;
|
||||||
|
return *this;
|
||||||
|
}
|
||||||
|
|
||||||
|
// moving ‹n› steps back is same as calling decrementation ‹n›-times, so we
|
||||||
|
// can just return a new iterator and subtract ‹n› from both coordinates in
|
||||||
|
// the matrix
|
||||||
|
diagonal_iter operator-(difference_type n) const
|
||||||
|
{
|
||||||
|
return diagonal_iter { m, x - n, y - n };
|
||||||
|
}
|
||||||
|
|
||||||
|
// here we assume that we are given two iterators on the same diagonal
|
||||||
|
difference_type operator-(const diagonal_iter& rhs) const
|
||||||
|
{
|
||||||
|
assert(m == rhs.m);
|
||||||
|
return x - rhs.x;
|
||||||
|
}
|
||||||
|
|
||||||
|
// counterpart of moving ‹n› steps backwards
|
||||||
|
diagonal_iter operator+(difference_type n) const
|
||||||
|
{
|
||||||
|
return diagonal_iter { m, x + n, y + n };
|
||||||
|
}
|
||||||
|
|
||||||
|
// we compare the coordinates, and also assume that those 2 iterators are
|
||||||
|
// lying on the same diagonal
|
||||||
|
bool operator<(const diagonal_iter& rhs) const
|
||||||
|
{
|
||||||
|
assert(m == rhs.m);
|
||||||
|
return x < rhs.x && y < rhs.y;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|
||||||
|
At this point we could probably try and compile it, right? If we do so, we will
|
||||||
|
get yelled at by a compiler for the following reasons:
|
||||||
|
```
|
||||||
|
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1792:11: error: object of type 'diagonal<int>::diagonal_iter' cannot be assigned because its copy assignment operator is implicitly deleted [clang-diagnostic-error]
|
||||||
|
__last = __next;
|
||||||
|
^
|
||||||
|
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1817:11: note: in instantiation of function template specialization 'std::__unguarded_linear_insert<diagonal<int>::diagonal_iter, __gnu_cxx::__ops::_Val_less_iter>' requested here
|
||||||
|
std::__unguarded_linear_insert(__i,
|
||||||
|
^
|
||||||
|
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1849:9: note: in instantiation of function template specialization 'std::__insertion_sort<diagonal<int>::diagonal_iter, __gnu_cxx::__ops::_Iter_less_iter>' requested here
|
||||||
|
std::__insertion_sort(__first, __first + int(_S_threshold), __comp);
|
||||||
|
^
|
||||||
|
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1940:9: note: in instantiation of function template specialization 'std::__final_insertion_sort<diagonal<int>::diagonal_iter, __gnu_cxx::__ops::_Iter_less_iter>' requested here
|
||||||
|
std::__final_insertion_sort(__first, __last, __comp);
|
||||||
|
^
|
||||||
|
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:4820:12: note: in instantiation of function template specialization 'std::__sort<diagonal<int>::diagonal_iter, __gnu_cxx::__ops::_Iter_less_iter>' requested here
|
||||||
|
std::__sort(__first, __last, __gnu_cxx::__ops::__iter_less_iter());
|
||||||
|
^
|
||||||
|
matrix-sort.cpp:161:18: note: in instantiation of function template specialization 'std::sort<diagonal<int>::diagonal_iter>' requested here
|
||||||
|
std::sort(d.begin(), d.end());
|
||||||
|
^
|
||||||
|
matrix-sort.cpp:17:19: note: copy assignment operator of 'diagonal_iter' is implicitly deleted because field 'm' is of reference type 'diagonal<int>::matrix_t &' (aka 'vector<std::vector<int>> &')
|
||||||
|
matrix_t& m;
|
||||||
|
^
|
||||||
|
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1830:2: error: no matching function for call to '__unguarded_linear_insert' [clang-diagnostic-error]
|
||||||
|
std::__unguarded_linear_insert(__i,
|
||||||
|
^~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
|
||||||
|
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1850:9: note: in instantiation of function template specialization 'std::__unguarded_insertion_sort<diagonal<int>::diagonal_iter, __gnu_cxx::__ops::_Iter_less_iter>' requested here
|
||||||
|
std::__unguarded_insertion_sort(__first + int(_S_threshold), __last,
|
||||||
|
^
|
||||||
|
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1940:9: note: in instantiation of function template specialization 'std::__final_insertion_sort<diagonal<int>::diagonal_iter, __gnu_cxx::__ops::_Iter_less_iter>' requested here
|
||||||
|
std::__final_insertion_sort(__first, __last, __comp);
|
||||||
|
^
|
||||||
|
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:4820:12: note: in instantiation of function template specialization 'std::__sort<diagonal<int>::diagonal_iter, __gnu_cxx::__ops::_Iter_less_iter>' requested here
|
||||||
|
std::__sort(__first, __last, __gnu_cxx::__ops::__iter_less_iter());
|
||||||
|
^
|
||||||
|
matrix-sort.cpp:161:18: note: in instantiation of function template specialization 'std::sort<diagonal<int>::diagonal_iter>' requested here
|
||||||
|
std::sort(d.begin(), d.end());
|
||||||
|
^
|
||||||
|
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1782:5: note: candidate template ignored: substitution failure [with _RandomAccessIterator = diagonal<int>::diagonal_iter, _Compare = __gnu_cxx::__ops::_Val_less_iter]
|
||||||
|
__unguarded_linear_insert(_RandomAccessIterator __last,
|
||||||
|
^
|
||||||
|
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1923:11: error: object of type 'diagonal<int>::diagonal_iter' cannot be assigned because its copy assignment operator is implicitly deleted [clang-diagnostic-error]
|
||||||
|
__last = __cut;
|
||||||
|
^
|
||||||
|
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1937:9: note: in instantiation of function template specialization 'std::__introsort_loop<diagonal<int>::diagonal_iter, long, __gnu_cxx::__ops::_Iter_less_iter>' requested here
|
||||||
|
std::__introsort_loop(__first, __last,
|
||||||
|
^
|
||||||
|
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:4820:12: note: in instantiation of function template specialization 'std::__sort<diagonal<int>::diagonal_iter, __gnu_cxx::__ops::_Iter_less_iter>' requested here
|
||||||
|
std::__sort(__first, __last, __gnu_cxx::__ops::__iter_less_iter());
|
||||||
|
^
|
||||||
|
matrix-sort.cpp:161:18: note: in instantiation of function template specialization 'std::sort<diagonal<int>::diagonal_iter>' requested here
|
||||||
|
std::sort(d.begin(), d.end());
|
||||||
|
^
|
||||||
|
matrix-sort.cpp:17:19: note: copy assignment operator of 'diagonal_iter' is implicitly deleted because field 'm' is of reference type 'diagonal<int>::matrix_t &' (aka 'vector<std::vector<int>> &')
|
||||||
|
matrix_t& m;
|
||||||
|
^
|
||||||
|
```
|
||||||
|
|
||||||
|
That's a lot of noise, isn't it? Let's focus on the important parts:
|
||||||
|
```
|
||||||
|
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1792:11: error: object of type 'diagonal<int>::diagonal_iter' cannot be assigned because its copy assignment operator is implicitly deleted [clang-diagnostic-error]
|
||||||
|
…
|
||||||
|
matrix-sort.cpp:17:19: note: copy assignment operator of 'diagonal_iter' is implicitly deleted because field 'm' is of reference type 'diagonal<int>::matrix_t &' (aka 'vector<std::vector<int>> &')
|
||||||
|
matrix_t& m;
|
||||||
|
^
|
||||||
|
```
|
||||||
|
|
||||||
|
Ah! We have a reference in our iterator, and this prevents us from having a copy
|
||||||
|
assignment operator (that is used “somewhere” in the sorting algorithm). Well…
|
||||||
|
Let's just wrap it!
|
||||||
|
```diff
|
||||||
|
# we need to keep a different type than reference
|
||||||
|
- matrix_t& m;
|
||||||
|
+ std::reference_wrapper<matrix_t> m;
|
||||||
|
|
||||||
|
# in comparison we need to get the reference out of the wrapper first
|
||||||
|
- return x == rhs.x && y == rhs.y && m == rhs.m;
|
||||||
|
+ return x == rhs.x && y == rhs.y && m.get() == rhs.m.get();
|
||||||
|
|
||||||
|
# same when we return a reference to the “cell” in the matrix
|
||||||
|
- reference operator*() const { return m[y][x]; }
|
||||||
|
+ reference operator*() const { return m.get()[y][x]; }
|
||||||
|
|
||||||
|
# and finally in the assertions that we set for the “distance” and “less than”
|
||||||
|
- assert(m == rhs.m);
|
||||||
|
+ assert(m.get() == rhs.m.get());
|
||||||
|
```
|
||||||
|
|
||||||
|
We're done now! We have written an iterator over diagonals for a 2D `vector`. You can have a look at the final result [here](pathname:///files/blog/leetcode/sort-matrix-diagonally/matrix-sort.cpp).
|
||||||
|
|
||||||
|
[^1]: just because I'm used to it and don't care about your opinion ;)
|
||||||
|
[^2]: exercise at your own risk
|
||||||
|
[^3]: me in 5 minutes in fact, but don't make me scared
|
||||||
|
[^4]: me in the next section…
|
||||||
16
static/files/blog/leetcode/sort-matrix-diagonally/makefile
Normal file
16
static/files/blog/leetcode/sort-matrix-diagonally/makefile
Normal file
|
|
@ -0,0 +1,16 @@
|
||||||
|
CXX=clang++
|
||||||
|
CXXFLAGS=-std=c++20 -Wall -Wextra -Werror -g -pedantic
|
||||||
|
|
||||||
|
test: matrix-sort
|
||||||
|
./matrix-sort
|
||||||
|
|
||||||
|
matrix-sort: format tidy
|
||||||
|
$(CXX) $(CXXFLAGS) matrix-sort.cpp -o matrix-sort
|
||||||
|
|
||||||
|
format:
|
||||||
|
clang-format -i -style=webkit *.cpp
|
||||||
|
|
||||||
|
tidy:
|
||||||
|
clang-tidy *.cpp -- $(CXXFLAGS)
|
||||||
|
|
||||||
|
.PHONY: matrix-sort format tidy
|
||||||
|
|
@ -0,0 +1,229 @@
|
||||||
|
#include <algorithm>
|
||||||
|
#include <cassert>
|
||||||
|
#include <vector>
|
||||||
|
|
||||||
|
using matrix = std::vector<std::vector<int>>;
|
||||||
|
|
||||||
|
template <typename T>
|
||||||
|
class diagonal {
|
||||||
|
using matrix_t = std::vector<std::vector<T>>;
|
||||||
|
|
||||||
|
matrix_t& matrix;
|
||||||
|
std::size_t x;
|
||||||
|
std::size_t y;
|
||||||
|
|
||||||
|
class diagonal_iter {
|
||||||
|
// we need to keep reference to the matrix itself
|
||||||
|
std::reference_wrapper<matrix_t> m;
|
||||||
|
|
||||||
|
// we need to be able to tell our current position
|
||||||
|
std::size_t x;
|
||||||
|
std::size_t y;
|
||||||
|
|
||||||
|
public:
|
||||||
|
using difference_type = std::ptrdiff_t;
|
||||||
|
using value_type = T;
|
||||||
|
using pointer = T*;
|
||||||
|
using reference = T&;
|
||||||
|
using iterator_category = std::random_access_iterator_tag;
|
||||||
|
|
||||||
|
diagonal_iter(matrix_t& matrix,
|
||||||
|
std::size_t x,
|
||||||
|
std::size_t y)
|
||||||
|
: m(matrix)
|
||||||
|
, x(x)
|
||||||
|
, y(y)
|
||||||
|
{
|
||||||
|
}
|
||||||
|
|
||||||
|
bool operator==(const diagonal_iter& rhs) const
|
||||||
|
{
|
||||||
|
return x == rhs.x && y == rhs.y && m.get() == rhs.m.get();
|
||||||
|
}
|
||||||
|
|
||||||
|
diagonal_iter& operator++()
|
||||||
|
{
|
||||||
|
// we are moving along the diagonal, so we increment both ‹x› and ‹y›
|
||||||
|
// at the same time
|
||||||
|
x++;
|
||||||
|
y++;
|
||||||
|
return *this;
|
||||||
|
}
|
||||||
|
|
||||||
|
reference operator*() const { return m.get()[y][x]; }
|
||||||
|
|
||||||
|
// exactly opposite to the incrementation
|
||||||
|
diagonal_iter operator--()
|
||||||
|
{
|
||||||
|
x--;
|
||||||
|
y--;
|
||||||
|
return *this;
|
||||||
|
}
|
||||||
|
|
||||||
|
// moving ‹n› steps back is same as calling decrementation ‹n›-times, so
|
||||||
|
// we can just return a new iterator and subtract ‹n› from both
|
||||||
|
// coordinates in the matrix
|
||||||
|
diagonal_iter operator-(difference_type n) const
|
||||||
|
{
|
||||||
|
return diagonal_iter { m, x - n, y - n };
|
||||||
|
}
|
||||||
|
|
||||||
|
// here we assume that we are given two iterators on the same diagonal
|
||||||
|
difference_type operator-(const diagonal_iter& rhs) const
|
||||||
|
{
|
||||||
|
assert(m.get() == rhs.m.get());
|
||||||
|
return x - rhs.x;
|
||||||
|
}
|
||||||
|
|
||||||
|
// counterpart of moving ‹n› steps backwards
|
||||||
|
diagonal_iter operator+(difference_type n) const
|
||||||
|
{
|
||||||
|
return diagonal_iter { m, x + n, y + n };
|
||||||
|
}
|
||||||
|
|
||||||
|
// we compare the coordinates, and also assume that those 2 iterators are
|
||||||
|
// lying on the same diagonal
|
||||||
|
bool operator<(const diagonal_iter& rhs) const
|
||||||
|
{
|
||||||
|
assert(m.get() == rhs.m.get());
|
||||||
|
return x < rhs.x && y < rhs.y;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
|
||||||
|
public:
|
||||||
|
diagonal(matrix_t& matrix, std::size_t x, std::size_t y)
|
||||||
|
: matrix(matrix)
|
||||||
|
, x(x)
|
||||||
|
, y(y)
|
||||||
|
{
|
||||||
|
}
|
||||||
|
|
||||||
|
diagonal_iter begin() const { return diagonal_iter { matrix, x, y }; }
|
||||||
|
|
||||||
|
diagonal_iter end() const
|
||||||
|
{
|
||||||
|
auto max_x = matrix[y].size();
|
||||||
|
auto max_y = matrix.size();
|
||||||
|
|
||||||
|
// we need to find the distance in which we get out of bounds (either in
|
||||||
|
// column or row)
|
||||||
|
auto steps = std::min(max_x - x, max_y - y);
|
||||||
|
|
||||||
|
return diagonal_iter { matrix, x + steps, y + steps };
|
||||||
|
}
|
||||||
|
};
|
||||||
|
|
||||||
|
template <typename T>
|
||||||
|
class diagonals {
|
||||||
|
using matrix_t = std::vector<std::vector<T>>;
|
||||||
|
|
||||||
|
class diagonals_iter {
|
||||||
|
matrix_t& m;
|
||||||
|
std::size_t x;
|
||||||
|
std::size_t y;
|
||||||
|
|
||||||
|
public:
|
||||||
|
diagonals_iter(matrix_t& matrix, std::size_t x, std::size_t y)
|
||||||
|
: m(matrix)
|
||||||
|
, x(x)
|
||||||
|
, y(y)
|
||||||
|
{
|
||||||
|
}
|
||||||
|
|
||||||
|
bool operator!=(const diagonals_iter& rhs) const
|
||||||
|
{
|
||||||
|
// iterators are not equal if they reference different matrices, or
|
||||||
|
// their positions differ
|
||||||
|
return x != rhs.x || y != rhs.y || m != rhs.m;
|
||||||
|
}
|
||||||
|
|
||||||
|
diagonals_iter& operator++()
|
||||||
|
{
|
||||||
|
if (y != 0) {
|
||||||
|
// iterating through diagonals down the first column
|
||||||
|
y++;
|
||||||
|
return *this;
|
||||||
|
}
|
||||||
|
|
||||||
|
// iterating the diagonals along the first row
|
||||||
|
x++;
|
||||||
|
if (x == m.front().size()) {
|
||||||
|
// switching to diagonals in the first column
|
||||||
|
x = 0;
|
||||||
|
y++;
|
||||||
|
}
|
||||||
|
|
||||||
|
return *this;
|
||||||
|
}
|
||||||
|
|
||||||
|
diagonal<T> operator*() const { return diagonal { m, x, y }; }
|
||||||
|
};
|
||||||
|
|
||||||
|
matrix_t& _matrix;
|
||||||
|
|
||||||
|
public:
|
||||||
|
diagonals(matrix_t& m)
|
||||||
|
: _matrix(m)
|
||||||
|
{
|
||||||
|
}
|
||||||
|
diagonals_iter begin() { return diagonals_iter { _matrix, 0, 0 }; }
|
||||||
|
diagonals_iter end() { return diagonals_iter { _matrix, 0, _matrix.size() }; }
|
||||||
|
};
|
||||||
|
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
matrix diagonalSort(matrix mat)
|
||||||
|
{
|
||||||
|
// we iterate over the diagonals
|
||||||
|
for (auto d : diagonals(mat)) {
|
||||||
|
// and we sort each diagonal
|
||||||
|
std::sort(d.begin(), d.end());
|
||||||
|
}
|
||||||
|
|
||||||
|
// we take the matrix by copy, so we can sort in-situ and return the copy
|
||||||
|
// that we sorted
|
||||||
|
return mat;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
|
||||||
|
static void test_case_1()
|
||||||
|
{
|
||||||
|
// Input: mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
|
||||||
|
// Output: [[1,1,1,1],[1,2,2,2],[1,2,3,3]]
|
||||||
|
|
||||||
|
Solution s;
|
||||||
|
assert((s.diagonalSort(std::vector { std::vector { 3, 3, 1, 1 },
|
||||||
|
std::vector { 2, 2, 1, 2 },
|
||||||
|
std::vector { 1, 1, 1, 2 } })
|
||||||
|
== std::vector { std::vector { 1, 1, 1, 1 },
|
||||||
|
std::vector { 1, 2, 2, 2 },
|
||||||
|
std::vector { 1, 2, 3, 3 } }));
|
||||||
|
}
|
||||||
|
|
||||||
|
static void test_case_2()
|
||||||
|
{
|
||||||
|
// Input: mat =
|
||||||
|
// [[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]]
|
||||||
|
// Output:
|
||||||
|
// [[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]
|
||||||
|
|
||||||
|
Solution s;
|
||||||
|
assert((s.diagonalSort(std::vector { std::vector { 11, 25, 66, 1, 69, 7 },
|
||||||
|
std::vector { 23, 55, 17, 45, 15, 52 },
|
||||||
|
std::vector { 75, 31, 36, 44, 58, 8 },
|
||||||
|
std::vector { 22, 27, 33, 25, 68, 4 },
|
||||||
|
std::vector { 84, 28, 14, 11, 5, 50 } })
|
||||||
|
== std::vector { std::vector { 5, 17, 4, 1, 52, 7 },
|
||||||
|
std::vector { 11, 11, 25, 45, 8, 69 },
|
||||||
|
std::vector { 14, 23, 25, 44, 58, 15 },
|
||||||
|
std::vector { 22, 27, 31, 36, 50, 66 },
|
||||||
|
std::vector { 84, 28, 75, 33, 55, 68 } }));
|
||||||
|
}
|
||||||
|
|
||||||
|
int main()
|
||||||
|
{
|
||||||
|
test_case_1();
|
||||||
|
test_case_2();
|
||||||
|
|
||||||
|
return 0;
|
||||||
|
}
|
||||||
Loading…
Add table
Add a link
Reference in a new issue