Sometimes some words like "localization" or "internationalization" are so long that writing them many times in one text is quite tiresome.
Let's consider a word too long, if its length is strictly more than 10 characters. All too long words should be replaced with a special abbreviation.
This abbreviation is made like this: we write down the first and the last letter of a word and between them we write the number of letters between the first and the last letters. That number is in decimal system and doesn't contain any leading zeroes.
Thus, "localization" will be spelt as "l10n", and "internationalization» will be spelt as "i18n".
You are suggested to automatize the process of changing the words with abbreviations. At that all too long words should be replaced by the abbreviation and the words that are not too long should not undergo any changes.
The first line contains an integer n (1 ≤ n ≤ 100). Each of the following n lines contains one word. All the words consist of lowercase Latin letters and possess the lengths of from 1 to 100 characters.
Print n lines. The i-th line should contain the result of replacing of the i-th word from the input data.
4
word
localization
internationalization
pneumonoultramicroscopicsilicovolcanoconiosis
word
l10n
i18n
p43s
A progress bar is an element of graphical interface that displays the progress of a process for this very moment before it is completed. Let's take a look at the following form of such a bar.
A bar is represented as n squares, located in line. To add clarity, let's number them with positive integers from 1 to n from the left to the right. Each square has saturation (ai for the i-th square), which is measured by an integer from 0 to k. When the bar for some i (1 ≤ i ≤ n) is displayed, squares 1, 2, ... , i - 1 has the saturation k, squares i + 1, i + 2, ... , n has the saturation 0, and the saturation of the square i can have any value from 0 to k.
So some first squares of the progress bar always have the saturation k. Some last squares always have the saturation 0. And there is no more than one square that has the saturation different from 0 and k.
The degree of the process's completion is measured in percents. Let the process be t% completed. Then the following inequation is fulfilled:
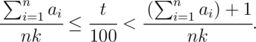
An example of such a bar can be seen on the picture.

For the given n, k, t determine the measures of saturation for all the squares ai of the progress bar.
We are given 3 space-separated integers n, k, t (1 ≤ n, k ≤ 100, 0 ≤ t ≤ 100).
Print n numbers. The i-th of them should be equal to ai.
10 10 54
10 10 10 10 10 4 0 0 0 0
11 13 37
13 13 13 13 0 0 0 0 0 0 0
There are n knights sitting at the Round Table at an equal distance from each other. Each of them is either in a good or in a bad mood.
Merlin, the wizard predicted to King Arthur that the next month will turn out to be particularly fortunate if the regular polygon can be found. On all vertices of the polygon knights in a good mood should be located. Otherwise, the next month will bring misfortunes.
A convex polygon is regular if all its sides have same length and all his angles are equal. In this problem we consider only regular polygons with at least 3 vertices, i. e. only nondegenerated.
On a picture below some examples of such polygons are present. Green points mean knights in a good mood. Red points mean ones in a bad mood.
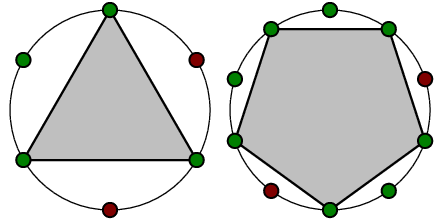
King Arthur knows the knights' moods. Help him find out if the next month will be fortunate or not.
The first line contains number n, which is the number of knights at the round table (3 ≤ n ≤ 105). The second line contains space-separated moods of all the n knights in the order of passing them around the table. "1" means that the knight is in a good mood an "0" means that he is in a bad mood.
Print "YES" without the quotes if the following month will turn out to be lucky. Otherwise, print "NO".
3
1 1 1
YES
6
1 0 1 1 1 0
YES
6
1 0 0 1 0 1
NO
Vasya has a pack of 54 cards (52 standard cards and 2 distinct jokers). That is all he has at the moment. Not to die from boredom, Vasya plays Solitaire with them.
Vasya lays out nm cards as a rectangle n × m. If there are jokers among them, then Vasya should change them with some of the rest of 54 - nm cards (which are not layed out) so that there were no jokers left. Vasya can pick the cards to replace the jokers arbitrarily. Remember, that each card presents in pack exactly once (i. e. in a single copy). Vasya tries to perform the replacements so that the solitaire was solved.
Vasya thinks that the solitaire is solved if after the jokers are replaced, there exist two non-overlapping squares 3 × 3, inside each of which all the cards either have the same suit, or pairwise different ranks.
Determine by the initial position whether the solitaire can be solved or not. If it can be solved, show the way in which it is possible.
The first line contains integers n and m (3 ≤ n, m ≤ 17, n × m ≤ 52). Next n lines contain m words each. Each word consists of two letters. The jokers are defined as "J1" and "J2" correspondingly. For the rest of the cards, the first letter stands for the rank and the second one — for the suit. The possible ranks are: "2", "3", "4", "5", "6", "7", "8", "9", "T", "J", "Q", "K" and "A". The possible suits are: "C", "D", "H" and "S". All the cards are different.
If the Solitaire can be solved, print on the first line "Solution exists." without the quotes. On the second line print in what way the jokers can be replaced. Three variants are possible:
- "There are no jokers.", if there are no jokers in the input data.
- "Replace Jx with y.", if there is one joker. x is its number, and y is the card it should be replaced with.
- "Replace J1 with x and J2 with y.", if both jokers are present in the input data. x and y here represent distinct cards with which one should replace the first and the second jokers correspondingly.
On the third line print the coordinates of the upper left corner of the first square 3 × 3 in the format "Put the first square to (r, c).", where r and c are the row and the column correspondingly. In the same manner print on the fourth line the coordinates of the second square 3 × 3 in the format "Put the second square to (r, c).".
If there are several solutions to that problem, print any of them.
If there are no solutions, print of the single line "No solution." without the quotes.
See the samples to understand the output format better.
4 6
2S 3S 4S 7S 8S AS
5H 6H 7H 5S TC AC
8H 9H TH 7C 8C 9C
2D 2C 3C 4C 5C 6C
No solution.
4 6
2S 3S 4S 7S 8S AS
5H 6H 7H J1 TC AC
8H 9H TH 7C 8C 9C
2D 2C 3C 4C 5C 6C
Solution exists.
Replace J1 with 2H.
Put the first square to (1, 1).
Put the second square to (2, 4).
4 6
2S 3S 4S 7S 8S AS
5H 6H 7H QC TC AC
8H 9H TH 7C 8C 9C
2D 2C 3C 4C 5C 6C
Solution exists.
There are no jokers.
Put the first square to (1, 1).
Put the second square to (2, 4).
The pretests cover all the possible output formats.
There is the following puzzle popular among nuclear physicists.
A reactor contains a set of n atoms of some chemical elements. We shall understand the phrase "atomic number" as the number of this atom's element in the periodic table of the chemical elements.
You are allowed to take any two different atoms and fuse a new one from them. That results in a new atom, whose number is equal to the sum of the numbers of original atoms. The fusion operation can be performed several times.
The aim is getting a new pregiven set of k atoms.
The puzzle's difficulty is that it is only allowed to fuse two atoms into one, it is not allowed to split an atom into several atoms. You are suggested to try to solve the puzzle.
The first line contains two integers n and k (1 ≤ k ≤ n ≤ 17). The second line contains space-separated symbols of elements of n atoms, which are available from the start. The third line contains space-separated symbols of elements of k atoms which need to be the result of the fusion. The symbols of the elements coincide with the symbols from the periodic table of the chemical elements. The atomic numbers do not exceed 100 (elements possessing larger numbers are highly unstable). Some atoms can have identical numbers (that is, there can be several atoms of the same element). The sum of numbers of initial atoms is equal to the sum of numbers of the atoms that need to be synthesized.
If it is impossible to synthesize the required atoms, print "NO" without the quotes. Otherwise, print on the first line «YES», and on the next k lines print the way of synthesizing each of k atoms as equations. Each equation has the following form: "x1+x2+...+xt->yi", where xj is the symbol of the element of some atom from the original set, and yi is the symbol of the element of some atom from the resulting set. Each atom from the input data should occur in the output data exactly one time. The order of summands in the equations, as well as the output order does not matter. If there are several solutions, print any of them. For a better understanding of the output format, see the samples.
10 3
Mn Co Li Mg C P F Zn Sc K
Sn Pt Y
YES
Mn+C+K->Sn
Co+Zn+Sc->Pt
Li+Mg+P+F->Y
2 1
H H
He
YES
H+H->He
2 2
Bk Fm
Cf Es
NO
The reactions from the first example possess the following form (the atomic number is written below and to the left of the element):
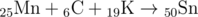
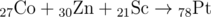
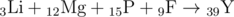
To find a periodic table of the chemical elements, you may use your favorite search engine.
The pretest set contains each of the first 100 elements of the periodic table at least once. You can use that information to check for misprints.


