Little girl Tanya is learning how to decrease a number by one, but she does it wrong with a number consisting of two or more digits. Tanya subtracts one from a number by the following algorithm:
- if the last digit of the number is non-zero, she decreases the number by one;
- if the last digit of the number is zero, she divides the number by 10 (i.e. removes the last digit).
You are given an integer number $$$n$$$. Tanya will subtract one from it $$$k$$$ times. Your task is to print the result after all $$$k$$$ subtractions.
It is guaranteed that the result will be positive integer number.
The first line of the input contains two integer numbers $$$n$$$ and $$$k$$$ ($$$2 \le n \le 10^9$$$, $$$1 \le k \le 50$$$) — the number from which Tanya will subtract and the number of subtractions correspondingly.
Print one integer number — the result of the decreasing $$$n$$$ by one $$$k$$$ times.
It is guaranteed that the result will be positive integer number.
512 4
50
1000000000 9
1
The first example corresponds to the following sequence: $$$512 \rightarrow 511 \rightarrow 510 \rightarrow 51 \rightarrow 50$$$.
Two-gram is an ordered pair (i.e. string of length two) of capital Latin letters. For example, "AZ", "AA", "ZA" — three distinct two-grams.
You are given a string $$$s$$$ consisting of $$$n$$$ capital Latin letters. Your task is to find any two-gram contained in the given string as a substring (i.e. two consecutive characters of the string) maximal number of times. For example, for string $$$s$$$ = "BBAABBBA" the answer is two-gram "BB", which contained in $$$s$$$ three times. In other words, find any most frequent two-gram.
Note that occurrences of the two-gram can overlap with each other.
The first line of the input contains integer number $$$n$$$ ($$$2 \le n \le 100$$$) — the length of string $$$s$$$. The second line of the input contains the string $$$s$$$ consisting of $$$n$$$ capital Latin letters.
Print the only line containing exactly two capital Latin letters — any two-gram contained in the given string $$$s$$$ as a substring (i.e. two consecutive characters of the string) maximal number of times.
7
ABACABA
AB
5
ZZZAA
ZZ
In the first example "BA" is also valid answer.
In the second example the only two-gram "ZZ" can be printed because it contained in the string "ZZZAA" two times.
You are given a sequence of integers of length $$$n$$$ and integer number $$$k$$$. You should print any integer number $$$x$$$ in the range of $$$[1; 10^9]$$$ (i.e. $$$1 \le x \le 10^9$$$) such that exactly $$$k$$$ elements of given sequence are less than or equal to $$$x$$$.
Note that the sequence can contain equal elements.
If there is no such $$$x$$$, print "-1" (without quotes).
The first line of the input contains integer numbers $$$n$$$ and $$$k$$$ ($$$1 \le n \le 2 \cdot 10^5$$$, $$$0 \le k \le n$$$). The second line of the input contains $$$n$$$ integer numbers $$$a_1, a_2, \dots, a_n$$$ ($$$1 \le a_i \le 10^9$$$) — the sequence itself.
Print any integer number $$$x$$$ from range $$$[1; 10^9]$$$ such that exactly $$$k$$$ elements of given sequence is less or equal to $$$x$$$.
If there is no such $$$x$$$, print "-1" (without quotes).
7 4
3 7 5 1 10 3 20
6
7 2
3 7 5 1 10 3 20
-1
In the first example $$$5$$$ is also a valid answer because the elements with indices $$$[1, 3, 4, 6]$$$ is less than or equal to $$$5$$$ and obviously less than or equal to $$$6$$$.
In the second example you cannot choose any number that only $$$2$$$ elements of the given sequence will be less than or equal to this number because $$$3$$$ elements of the given sequence will be also less than or equal to this number.
Polycarp likes to play with numbers. He takes some integer number $$$x$$$, writes it down on the board, and then performs with it $$$n - 1$$$ operations of the two kinds:
- divide the number $$$x$$$ by $$$3$$$ ($$$x$$$ must be divisible by $$$3$$$);
- multiply the number $$$x$$$ by $$$2$$$.
After each operation, Polycarp writes down the result on the board and replaces $$$x$$$ by the result. So there will be $$$n$$$ numbers on the board after all.
You are given a sequence of length $$$n$$$ — the numbers that Polycarp wrote down. This sequence is given in arbitrary order, i.e. the order of the sequence can mismatch the order of the numbers written on the board.
Your problem is to rearrange (reorder) elements of this sequence in such a way that it can match possible Polycarp's game in the order of the numbers written on the board. I.e. each next number will be exactly two times of the previous number or exactly one third of previous number.
It is guaranteed that the answer exists.
The first line of the input contatins an integer number $$$n$$$ ($$$2 \le n \le 100$$$) — the number of the elements in the sequence. The second line of the input contains $$$n$$$ integer numbers $$$a_1, a_2, \dots, a_n$$$ ($$$1 \le a_i \le 3 \cdot 10^{18}$$$) — rearranged (reordered) sequence that Polycarp can wrote down on the board.
Print $$$n$$$ integer numbers — rearranged (reordered) input sequence that can be the sequence that Polycarp could write down on the board.
It is guaranteed that the answer exists.
6
4 8 6 3 12 9
9 3 6 12 4 8
4
42 28 84 126
126 42 84 28
2
1000000000000000000 3000000000000000000
3000000000000000000 1000000000000000000
In the first example the given sequence can be rearranged in the following way: $$$[9, 3, 6, 12, 4, 8]$$$. It can match possible Polycarp's game which started with $$$x = 9$$$.
You are given an undirected graph consisting of $$$n$$$ vertices and $$$m$$$ edges. Your task is to find the number of connected components which are cycles.
Here are some definitions of graph theory.
An undirected graph consists of two sets: set of nodes (called vertices) and set of edges. Each edge connects a pair of vertices. All edges are bidirectional (i.e. if a vertex $$$a$$$ is connected with a vertex $$$b$$$, a vertex $$$b$$$ is also connected with a vertex $$$a$$$). An edge can't connect vertex with itself, there is at most one edge between a pair of vertices.
Two vertices $$$u$$$ and $$$v$$$ belong to the same connected component if and only if there is at least one path along edges connecting $$$u$$$ and $$$v$$$.
A connected component is a cycle if and only if its vertices can be reordered in such a way that:
- the first vertex is connected with the second vertex by an edge,
- the second vertex is connected with the third vertex by an edge,
- ...
- the last vertex is connected with the first vertex by an edge,
- all the described edges of a cycle are distinct.
A cycle doesn't contain any other edges except described above. By definition any cycle contains three or more vertices.
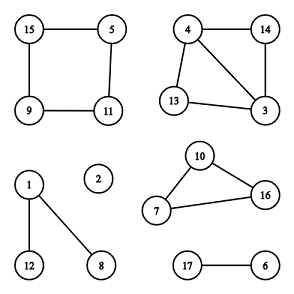 There are $$$6$$$ connected components, $$$2$$$ of them are cycles: $$$[7, 10, 16]$$$ and $$$[5, 11, 9, 15]$$$.
There are $$$6$$$ connected components, $$$2$$$ of them are cycles: $$$[7, 10, 16]$$$ and $$$[5, 11, 9, 15]$$$. The first line contains two integer numbers $$$n$$$ and $$$m$$$ ($$$1 \le n \le 2 \cdot 10^5$$$, $$$0 \le m \le 2 \cdot 10^5$$$) — number of vertices and edges.
The following $$$m$$$ lines contains edges: edge $$$i$$$ is given as a pair of vertices $$$v_i$$$, $$$u_i$$$ ($$$1 \le v_i, u_i \le n$$$, $$$u_i \ne v_i$$$). There is no multiple edges in the given graph, i.e. for each pair ($$$v_i, u_i$$$) there no other pairs ($$$v_i, u_i$$$) and ($$$u_i, v_i$$$) in the list of edges.
Print one integer — the number of connected components which are also cycles.
5 4
1 2
3 4
5 4
3 5
1
17 15
1 8
1 12
5 11
11 9
9 15
15 5
4 13
3 13
4 3
10 16
7 10
16 7
14 3
14 4
17 6
2
In the first example only component $$$[3, 4, 5]$$$ is also a cycle.
The illustration above corresponds to the second example.
You are given an integer array of length $$$n$$$.
You have to choose some subsequence of this array of maximum length such that this subsequence forms a increasing sequence of consecutive integers. In other words the required sequence should be equal to $$$[x, x + 1, \dots, x + k - 1]$$$ for some value $$$x$$$ and length $$$k$$$.
Subsequence of an array can be obtained by erasing some (possibly zero) elements from the array. You can erase any elements, not necessarily going successively. The remaining elements preserve their order. For example, for the array $$$[5, 3, 1, 2, 4]$$$ the following arrays are subsequences: $$$[3]$$$, $$$[5, 3, 1, 2, 4]$$$, $$$[5, 1, 4]$$$, but the array $$$[1, 3]$$$ is not.
The first line of the input containing integer number $$$n$$$ ($$$1 \le n \le 2 \cdot 10^5$$$) — the length of the array. The second line of the input containing $$$n$$$ integer numbers $$$a_1, a_2, \dots, a_n$$$ ($$$1 \le a_i \le 10^9$$$) — the array itself.
On the first line print $$$k$$$ — the maximum length of the subsequence of the given array that forms an increasing sequence of consecutive integers.
On the second line print the sequence of the indices of the any maximum length subsequence of the given array that forms an increasing sequence of consecutive integers.
7
3 3 4 7 5 6 8
4
2 3 5 6
6
1 3 5 2 4 6
2
1 4
4
10 9 8 7
1
1
9
6 7 8 3 4 5 9 10 11
6
1 2 3 7 8 9
All valid answers for the first example (as sequences of indices):
- $$$[1, 3, 5, 6]$$$
- $$$[2, 3, 5, 6]$$$
All valid answers for the second example:
- $$$[1, 4]$$$
- $$$[2, 5]$$$
- $$$[3, 6]$$$
All valid answers for the third example:
- $$$[1]$$$
- $$$[2]$$$
- $$$[3]$$$
- $$$[4]$$$
All valid answers for the fourth example:
- $$$[1, 2, 3, 7, 8, 9]$$$


