Anton likes to play chess, and so does his friend Danik.
Once they have played n games in a row. For each game it's known who was the winner — Anton or Danik. None of the games ended with a tie.
Now Anton wonders, who won more games, he or Danik? Help him determine this.
The first line of the input contains a single integer n (1 ≤ n ≤ 100 000) — the number of games played.
The second line contains a string s, consisting of n uppercase English letters 'A' and 'D' — the outcome of each of the games. The i-th character of the string is equal to 'A' if the Anton won the i-th game and 'D' if Danik won the i-th game.
If Anton won more games than Danik, print "Anton" (without quotes) in the only line of the output.
If Danik won more games than Anton, print "Danik" (without quotes) in the only line of the output.
If Anton and Danik won the same number of games, print "Friendship" (without quotes).
6
ADAAAA
Anton
7
DDDAADA
Danik
6
DADADA
Friendship
In the first sample, Anton won 6 games, while Danik — only 1. Hence, the answer is "Anton".
In the second sample, Anton won 3 games and Danik won 4 games, so the answer is "Danik".
In the third sample, both Anton and Danik won 3 games and the answer is "Friendship".
Recently Anton found a box with digits in his room. There are k2 digits 2, k3 digits 3, k5 digits 5 and k6 digits 6.
Anton's favorite integers are 32 and 256. He decided to compose this integers from digits he has. He wants to make the sum of these integers as large as possible. Help him solve this task!
Each digit can be used no more than once, i.e. the composed integers should contain no more than k2 digits 2, k3 digits 3 and so on. Of course, unused digits are not counted in the sum.
The only line of the input contains four integers k2, k3, k5 and k6 — the number of digits 2, 3, 5 and 6 respectively (0 ≤ k2, k3, k5, k6 ≤ 5·106).
Print one integer — maximum possible sum of Anton's favorite integers that can be composed using digits from the box.
5 1 3 4
800
1 1 1 1
256
In the first sample, there are five digits 2, one digit 3, three digits 5 and four digits 6. Anton can compose three integers 256 and one integer 32 to achieve the value 256 + 256 + 256 + 32 = 800. Note, that there is one unused integer 2 and one unused integer 6. They are not counted in the answer.
In the second sample, the optimal answer is to create on integer 256, thus the answer is 256.
Anton is playing a very interesting computer game, but now he is stuck at one of the levels. To pass to the next level he has to prepare n potions.
Anton has a special kettle, that can prepare one potions in x seconds. Also, he knows spells of two types that can faster the process of preparing potions.
- Spells of this type speed up the preparation time of one potion. There are m spells of this type, the i-th of them costs bi manapoints and changes the preparation time of each potion to ai instead of x.
- Spells of this type immediately prepare some number of potions. There are k such spells, the i-th of them costs di manapoints and instantly create ci potions.
Anton can use no more than one spell of the first type and no more than one spell of the second type, and the total number of manapoints spent should not exceed s. Consider that all spells are used instantly and right before Anton starts to prepare potions.
Anton wants to get to the next level as fast as possible, so he is interested in the minimum number of time he needs to spent in order to prepare at least n potions.
The first line of the input contains three integers n, m, k (1 ≤ n ≤ 2·109, 1 ≤ m, k ≤ 2·105) — the number of potions, Anton has to make, the number of spells of the first type and the number of spells of the second type.
The second line of the input contains two integers x and s (2 ≤ x ≤ 2·109, 1 ≤ s ≤ 2·109) — the initial number of seconds required to prepare one potion and the number of manapoints Anton can use.
The third line contains m integers ai (1 ≤ ai < x) — the number of seconds it will take to prepare one potion if the i-th spell of the first type is used.
The fourth line contains m integers bi (1 ≤ bi ≤ 2·109) — the number of manapoints to use the i-th spell of the first type.
There are k integers ci (1 ≤ ci ≤ n) in the fifth line — the number of potions that will be immediately created if the i-th spell of the second type is used. It's guaranteed that ci are not decreasing, i.e. ci ≤ cj if i < j.
The sixth line contains k integers di (1 ≤ di ≤ 2·109) — the number of manapoints required to use the i-th spell of the second type. It's guaranteed that di are not decreasing, i.e. di ≤ dj if i < j.
Print one integer — the minimum time one has to spent in order to prepare n potions.
20 3 2
10 99
2 4 3
20 10 40
4 15
10 80
20
20 3 2
10 99
2 4 3
200 100 400
4 15
100 800
200
In the first sample, the optimum answer is to use the second spell of the first type that costs 10 manapoints. Thus, the preparation time of each potion changes to 4 seconds. Also, Anton should use the second spell of the second type to instantly prepare 15 potions spending 80 manapoints. The total number of manapoints used is 10 + 80 = 90, and the preparation time is 4·5 = 20 seconds (15 potions were prepared instantly, and the remaining 5 will take 4 seconds each).
In the second sample, Anton can't use any of the spells, so he just prepares 20 potions, spending 10 seconds on each of them and the answer is 20·10 = 200.
Anton likes to play chess. Also, he likes to do programming. That is why he decided to write the program that plays chess. However, he finds the game on 8 to 8 board to too simple, he uses an infinite one instead.
The first task he faced is to check whether the king is in check. Anton doesn't know how to implement this so he asks you to help.
Consider that an infinite chess board contains one white king and the number of black pieces. There are only rooks, bishops and queens, as the other pieces are not supported yet. The white king is said to be in check if at least one black piece can reach the cell with the king in one move.
Help Anton and write the program that for the given position determines whether the white king is in check.
Remainder, on how do chess pieces move:
- Bishop moves any number of cells diagonally, but it can't "leap" over the occupied cells.
- Rook moves any number of cells horizontally or vertically, but it also can't "leap" over the occupied cells.
- Queen is able to move any number of cells horizontally, vertically or diagonally, but it also can't "leap".
The first line of the input contains a single integer n (1 ≤ n ≤ 500 000) — the number of black pieces.
The second line contains two integers x0 and y0 ( - 109 ≤ x0, y0 ≤ 109) — coordinates of the white king.
Then follow n lines, each of them contains a character and two integers xi and yi ( - 109 ≤ xi, yi ≤ 109) — type of the i-th piece and its position. Character 'B' stands for the bishop, 'R' for the rook and 'Q' for the queen. It's guaranteed that no two pieces occupy the same position.
The only line of the output should contains "YES" (without quotes) if the white king is in check and "NO" (without quotes) otherwise.
2
4 2
R 1 1
B 1 5
YES
2
4 2
R 3 3
B 1 5
NO
Picture for the first sample:

Picture for the second sample:

Anton is growing a tree in his garden. In case you forgot, the tree is a connected acyclic undirected graph.
There are n vertices in the tree, each of them is painted black or white. Anton doesn't like multicolored trees, so he wants to change the tree such that all vertices have the same color (black or white).
To change the colors Anton can use only operations of one type. We denote it as paint(v), where v is some vertex of the tree. This operation changes the color of all vertices u such that all vertices on the shortest path from v to u have the same color (including v and u). For example, consider the tree
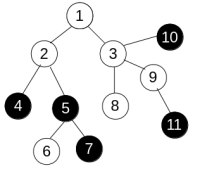
and apply operation paint(3) to get the following:
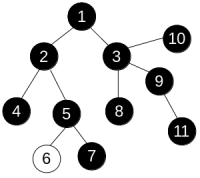
Anton is interested in the minimum number of operation he needs to perform in order to make the colors of all vertices equal.
The first line of the input contains a single integer n (1 ≤ n ≤ 200 000) — the number of vertices in the tree.
The second line contains n integers colori (0 ≤ colori ≤ 1) — colors of the vertices. colori = 0 means that the i-th vertex is initially painted white, while colori = 1 means it's initially painted black.
Then follow n - 1 line, each of them contains a pair of integers ui and vi (1 ≤ ui, vi ≤ n, ui ≠ vi) — indices of vertices connected by the corresponding edge. It's guaranteed that all pairs (ui, vi) are distinct, i.e. there are no multiple edges.
Print one integer — the minimum number of operations Anton has to apply in order to make all vertices of the tree black or all vertices of the tree white.
11
0 0 0 1 1 0 1 0 0 1 1
1 2
1 3
2 4
2 5
5 6
5 7
3 8
3 9
3 10
9 11
2
4
0 0 0 0
1 2
2 3
3 4
0
In the first sample, the tree is the same as on the picture. If we first apply operation paint(3) and then apply paint(6), the tree will become completely black, so the answer is 2.
In the second sample, the tree is already white, so there is no need to apply any operations and the answer is 0.
Anton goes to school, his favorite lessons are arraystudying. He usually solves all the tasks pretty fast, but this time the teacher gave him a complicated one: given two arrays b and c of length n, find array a, such that:
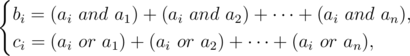
where a and b means bitwise AND, while a or b means bitwise OR.
Usually Anton is good in arraystudying, but this problem is too hard, so Anton asks you to help.
The first line of the input contains a single integers n (1 ≤ n ≤ 200 000) — the size of arrays b and c.
The second line contains n integers bi (0 ≤ bi ≤ 109) — elements of the array b.
Third line contains n integers ci (0 ≤ ci ≤ 109) — elements of the array c.
If there is no solution, print - 1.
Otherwise, the only line of the output should contain n non-negative integers ai — elements of the array a. If there are multiple possible solutions, you may print any of them.
4
6 8 4 4
16 22 10 10
3 5 1 1
5
8 25 14 7 16
19 6 9 4 25
-1


