Capitalization is writing a word with its first letter as a capital letter. Your task is to capitalize the given word.
Note, that during capitalization all the letters except the first one remains unchanged.
A single line contains a non-empty word. This word consists of lowercase and uppercase English letters. The length of the word will not exceed 103.
Output the given word after capitalization.
ApPLe
ApPLe
konjac
Konjac
You are given three positive integers x, y, n. Your task is to find the nearest fraction to fraction  whose denominator is no more than n.
whose denominator is no more than n.
Formally, you should find such pair of integers a, b (1 ≤ b ≤ n; 0 ≤ a) that the value 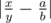 is as minimal as possible.
is as minimal as possible.
If there are multiple "nearest" fractions, choose the one with the minimum denominator. If there are multiple "nearest" fractions with the minimum denominator, choose the one with the minimum numerator.
A single line contains three integers x, y, n (1 ≤ x, y, n ≤ 105).
Print the required fraction in the format "a/b" (without quotes).
3 7 6
2/5
7 2 4
7/2
You are given two rectangles on a plane. The centers of both rectangles are located in the origin of coordinates (meaning the center of the rectangle's symmetry). The first rectangle's sides are parallel to the coordinate axes: the length of the side that is parallel to the Ox axis, equals w, the length of the side that is parallel to the Oy axis, equals h. The second rectangle can be obtained by rotating the first rectangle relative to the origin of coordinates by angle α.

Your task is to find the area of the region which belongs to both given rectangles. This region is shaded in the picture.
The first line contains three integers w, h, α (1 ≤ w, h ≤ 106; 0 ≤ α ≤ 180). Angle α is given in degrees.
In a single line print a real number — the area of the region which belongs to both given rectangles.
The answer will be considered correct if its relative or absolute error doesn't exceed 10 - 6.
1 1 45
0.828427125
6 4 30
19.668384925
The second sample has been drawn on the picture above.
Bike loves looking for the second maximum element in the sequence. The second maximum element in the sequence of distinct numbers x1, x2, ..., xk (k > 1) is such maximum element xj, that the following inequality holds: 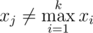 .
.
The lucky number of the sequence of distinct positive integers x1, x2, ..., xk (k > 1) is the number that is equal to the bitwise excluding OR of the maximum element of the sequence and the second maximum element of the sequence.
You've got a sequence of distinct positive integers s1, s2, ..., sn (n > 1). Let's denote sequence sl, sl + 1, ..., sr as s[l..r] (1 ≤ l < r ≤ n). Your task is to find the maximum number among all lucky numbers of sequences s[l..r].
Note that as all numbers in sequence s are distinct, all the given definitions make sence.
The first line contains integer n (1 < n ≤ 105). The second line contains n distinct integers s1, s2, ..., sn (1 ≤ si ≤ 109).
Print a single integer — the maximum lucky number among all lucky numbers of sequences s[l..r].
5
5 2 1 4 3
7
5
9 8 3 5 7
15
For the first sample you can choose s[4..5] = {4, 3} and its lucky number is (4 xor 3) = 7. You can also choose s[1..2].
For the second sample you must choose s[2..5] = {8, 3, 5, 7}.
Momiji has got a rooted tree, consisting of n nodes. The tree nodes are numbered by integers from 1 to n. The root has number 1. Momiji decided to play a game on this tree.
The game consists of several steps. On each step, Momiji chooses one of the remaining tree nodes (let's denote it by v) and removes all the subtree nodes with the root in node v from the tree. Node v gets deleted as well. The game finishes when the tree has no nodes left. In other words, the game finishes after the step that chooses the node number 1.
Each time Momiji chooses a new node uniformly among all the remaining nodes. Your task is to find the expectation of the number of steps in the described game.
The first line contains integer n (1 ≤ n ≤ 105) — the number of nodes in the tree. The next n - 1 lines contain the tree edges. The i-th line contains integers ai, bi (1 ≤ ai, bi ≤ n; ai ≠ bi) — the numbers of the nodes that are connected by the i-th edge.
It is guaranteed that the given graph is a tree.
Print a single real number — the expectation of the number of steps in the described game.
The answer will be considered correct if the absolute or relative error doesn't exceed 10 - 6.
2
1 2
1.50000000000000000000
3
1 2
1 3
2.00000000000000000000
In the first sample, there are two cases. One is directly remove the root and another is remove the root after one step. Thus the expected steps are:
In the second sample, things get more complex. There are two cases that reduce to the first sample, and one case cleaned at once. Thus the expected steps are:


