Suneet has three digits $$$a$$$, $$$b$$$, and $$$c$$$.
Since math isn't his strongest point, he asks you to determine if you can choose any two digits to make a sum greater or equal to $$$10$$$.
Output "YES" if there is such a pair, and "NO" otherwise.
The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 1000$$$) — the number of test cases.
The only line of each test case contains three digits $$$a$$$, $$$b$$$, $$$c$$$ ($$$0 \leq a, b, c \leq 9$$$).
For each test case, output "YES" if such a pair exists, and "NO" otherwise.
You can output the answer in any case (for example, the strings "yEs", "yes", "Yes" and "YES" will be recognized as a positive answer).
58 1 24 4 59 9 90 0 08 5 3
YES NO YES NO YES
For the first test case, by choosing the digits $$$8$$$ and $$$2$$$ we can obtain a sum of $$$8 + 2 = 10$$$ which satisfies the condition, thus the output should be "YES".
For the second test case, any combination of chosen digits won't be at least $$$10$$$, thus the output should be "NO" (note that we can not choose the digit on the same position twice).
For the third test case, any combination of chosen digits will have a sum equal to $$$18$$$, thus the output should be "YES".
In the game show "Ten Words of Wisdom", there are $$$n$$$ participants numbered from $$$1$$$ to $$$n$$$, each of whom submits one response. The $$$i$$$-th response is $$$a_i$$$ words long and has quality $$$b_i$$$. No two responses have the same quality, and at least one response has length at most $$$10$$$.
The winner of the show is the response which has the highest quality out of all responses that are not longer than $$$10$$$ words. Which response is the winner?
The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 100$$$) — the number of test cases.
The first line of each test case contains a single integer $$$n$$$ ($$$1 \leq n \leq 50$$$) — the number of responses.
Then $$$n$$$ lines follow, the $$$i$$$-th of which contains two integers $$$a_i$$$ and $$$b_i$$$ ($$$1 \leq a_i, b_i \leq 50$$$) — the number of words and the quality of the $$$i$$$-th response, respectively.
Additional constraints on the input: in each test case, at least one value of $$$i$$$ satisfies $$$a_i \leq 10$$$, and all values of $$$b_i$$$ are distinct.
For each test case, output a single line containing one integer $$$x$$$ ($$$1 \leq x \leq n$$$) — the winner of the show, according to the rules given in the statement.
It can be shown that, according to the constraints in the statement, exactly one winner exists for each test case.
357 212 59 39 410 131 23 45 611 43
4 3 1
In the first test case, the responses provided are as follows:
- Response 1: $$$7$$$ words, quality $$$2$$$
- Response 2: $$$12$$$ words, quality $$$5$$$
- Response 3: $$$9$$$ words, quality $$$3$$$
- Response 4: $$$9$$$ words, quality $$$4$$$
- Response 5: $$$10$$$ words, quality $$$1$$$
We can see that the responses with indices $$$1$$$, $$$3$$$, $$$4$$$, and $$$5$$$ have lengths not exceeding $$$10$$$ words. Out of these responses, the winner is the one with the highest quality.
Comparing the qualities, we find that:
- Response 1 has quality $$$2$$$.
- Response 3 has quality $$$3$$$.
- Response 4 has quality $$$4$$$.
- Response 5 has quality $$$1$$$.
Among these responses, Response 4 has the highest quality.
On an $$$8 \times 8$$$ grid of dots, a word consisting of lowercase Latin letters is written vertically in one column, from top to bottom. What is it?
The input consists of multiple test cases. The first line of the input contains a single integer $$$t$$$ ($$$1 \leq t \leq 1000$$$) — the number of test cases.
Each test case consists of $$$8$$$ lines, each containing $$$8$$$ characters. Each character in the grid is either $$$\texttt{.}$$$ (representing a dot) or a lowercase Latin letter ($$$\texttt{a}$$$–$$$\texttt{z}$$$).
The word lies entirely in a single column and is continuous from the beginning to the ending (without gaps). See the sample input for better understanding.
For each test case, output a single line containing the word made up of lowercase Latin letters ($$$\texttt{a}$$$–$$$\texttt{z}$$$) that is written vertically in one column from top to bottom.
5...................................i.....................................l.......o.......s.......t....................................................................t.......h.......e................................................g.......a.......m.......ea.......a.......a.......a.......a.......a.......a.......a.......
i lost the game aaaaaaaa
You are the author of a Codeforces round and have prepared $$$n$$$ problems you are going to set, problem $$$i$$$ having difficulty $$$a_i$$$. You will do the following process:
- remove some (possibly zero) problems from the list;
- rearrange the remaining problems in any order you wish.
A round is considered balanced if and only if the absolute difference between the difficulty of any two consecutive problems is at most $$$k$$$ (less or equal than $$$k$$$).
What is the minimum number of problems you have to remove so that an arrangement of problems is balanced?
The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 1000$$$) — the number of test cases.
The first line of each test case contains two positive integers $$$n$$$ ($$$1 \leq n \leq 2 \cdot 10^5$$$) and $$$k$$$ ($$$1 \leq k \leq 10^9$$$) — the number of problems, and the maximum allowed absolute difference between consecutive problems.
The second line of each test case contains $$$n$$$ space-separated integers $$$a_i$$$ ($$$1 \leq a_i \leq 10^9$$$) — the difficulty of each problem.
Note that the sum of $$$n$$$ over all test cases doesn't exceed $$$2 \cdot 10^5$$$.
For each test case, output a single integer — the minimum number of problems you have to remove so that an arrangement of problems is balanced.
75 11 2 4 5 61 2108 317 3 1 20 12 5 17 124 22 4 6 85 32 3 19 10 83 41 10 58 18 3 1 4 5 10 7 3
2 0 5 0 3 1 4
For the first test case, we can remove the first $$$2$$$ problems and construct a set using problems with the difficulties $$$[4, 5, 6]$$$, with difficulties between adjacent problems equal to $$$|5 - 4| = 1 \leq 1$$$ and $$$|6 - 5| = 1 \leq 1$$$.
For the second test case, we can take the single problem and compose a round using the problem with difficulty $$$10$$$.
Mircea has $$$n$$$ pictures. The $$$i$$$-th picture is a square with a side length of $$$s_i$$$ centimeters.
He mounted each picture on a square piece of cardboard so that each picture has a border of $$$w$$$ centimeters of cardboard on all sides. In total, he used $$$c$$$ square centimeters of cardboard. Given the picture sizes and the value $$$c$$$, can you find the value of $$$w$$$?
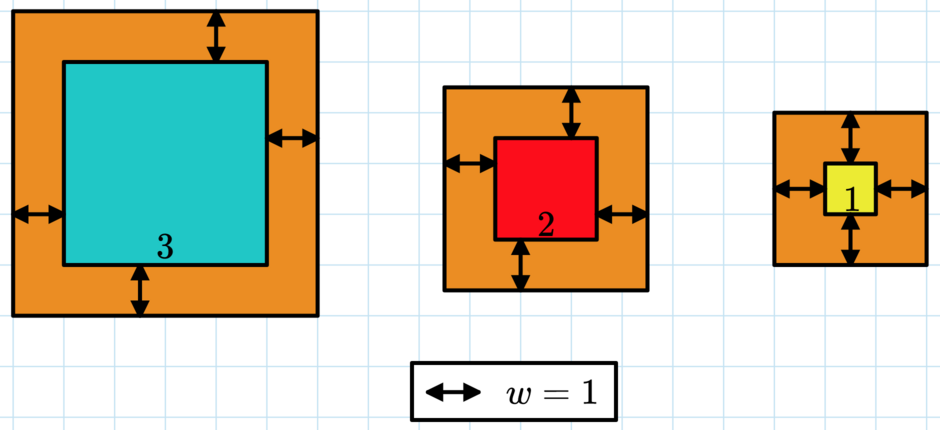 A picture of the first test case. Here $$$c = 50 = 5^2 + 4^2 + 3^2$$$, so $$$w=1$$$ is the answer.
A picture of the first test case. Here $$$c = 50 = 5^2 + 4^2 + 3^2$$$, so $$$w=1$$$ is the answer. Please note that the piece of cardboard goes behind each picture, not just the border.
The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 1000$$$) — the number of test cases.
The first line of each test case contains two positive integers $$$n$$$ ($$$1 \leq n \leq 2 \cdot 10^5$$$) and $$$c$$$ ($$$1 \leq c \leq 10^{18}$$$) — the number of paintings, and the amount of used square centimeters of cardboard.
The second line of each test case contains $$$n$$$ space-separated integers $$$s_i$$$ ($$$1 \leq s_i \leq 10^4$$$) — the sizes of the paintings.
The sum of $$$n$$$ over all test cases doesn't exceed $$$2 \cdot 10^5$$$.
Additional constraint on the input: Such an integer $$$w$$$ exists for each test case.
Please note, that some of the input for some test cases won't fit into 32-bit integer type, so you should use at least 64-bit integer type in your programming language (like long long for C++).
For each test case, output a single integer — the value of $$$w$$$ ($$$w \geq 1$$$) which was used to use exactly $$$c$$$ squared centimeters of cardboard.
10 3 50 3 2 1 1 100 6 5 500 2 2 2 2 2 2 365 3 4 2 469077255466389 10000 2023 10 635472106413848880 9181 4243 7777 1859 2017 4397 14 9390 2245 7225 7 176345687772781240 9202 9407 9229 6257 7743 5738 7966 14 865563946464579627 3654 5483 1657 7571 1639 9815 122 9468 3079 2666 5498 4540 7861 5384 19 977162053008871403 9169 9520 9209 9013 9300 9843 9933 9454 9960 9167 9964 9701 9251 9404 9462 9277 9661 9164 9161 18 886531871815571953 2609 10 5098 9591 949 8485 6385 4586 1064 5412 6564 8460 2245 6552 5089 8353 3803 3764
1 2 4 5 7654321 126040443 79356352 124321725 113385729 110961227
The first test case is explained in the statement.
For the second test case, the chosen $$$w$$$ was $$$2$$$, thus the only cardboard covers an area of $$$c = (2 \cdot 2 + 6)^2 = 10^2 = 100$$$ squared centimeters.
For the third test case, the chosen $$$w$$$ was $$$4$$$, which obtains the covered area $$$c = (2 \cdot 4 + 2)^2 \times 5 = 10^2 \times 5 = 100 \times 5 = 500$$$ squared centimeters.
Mihai and Slavic were looking at a group of $$$n$$$ frogs, numbered from $$$1$$$ to $$$n$$$, all initially located at point $$$0$$$. Frog $$$i$$$ has a hop length of $$$a_i$$$.
Each second, frog $$$i$$$ hops $$$a_i$$$ units forward. Before any frogs start hopping, Slavic and Mihai can place exactly one trap in a coordinate in order to catch all frogs that will ever pass through the corresponding coordinate.
However, the children can't go far away from their home so they can only place a trap in the first $$$n$$$ points (that is, in a point with a coordinate between $$$1$$$ and $$$n$$$) and the children can't place a trap in point $$$0$$$ since they are scared of frogs.
Can you help Slavic and Mihai find out what is the maximum number of frogs they can catch using a trap?
The first line of the input contains a single integer $$$t$$$ ($$$1 \le t \le 100$$$) — the number of test cases. The description of test cases follows.
The first line of each test case contains a single integer $$$n$$$ ($$$1 \leq n \leq 2 \cdot 10^5$$$) — the number of frogs, which equals the distance Slavic and Mihai can travel to place a trap.
The second line of each test case contains $$$n$$$ integers $$$a_1, \ldots, a_n$$$ ($$$1 \leq a_i \leq 10^9$$$) — the lengths of the hops of the corresponding frogs.
It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$2 \cdot 10^5$$$.
For each test case output a single integer — the maximum number of frogs Slavic and Mihai can catch using a trap.
751 2 3 4 532 2 263 1 3 4 9 1091 3 2 4 2 3 7 8 511087 11 6 8 12 4 4 8109 11 9 12 1 7 2 5 8 10
3 3 3 5 0 4 4
In the first test case, the frogs will hop as follows:
- Frog 1: $$$0 \to 1 \to 2 \to 3 \to \mathbf{\color{red}{4}} \to \cdots$$$
- Frog 2: $$$0 \to 2 \to \mathbf{\color{red}{4}} \to 6 \to 8 \to \cdots$$$
- Frog 3: $$$0 \to 3 \to 6 \to 9 \to 12 \to \cdots$$$
- Frog 4: $$$0 \to \mathbf{\color{red}{4}} \to 8 \to 12 \to 16 \to \cdots$$$
- Frog 5: $$$0 \to 5 \to 10 \to 15 \to 20 \to \cdots$$$
In the second test case, Slavic and Mihai can put a trap at coordinate $$$2$$$ and catch all three frogs instantly.
A compass points directly toward the morning star. It can only point in one of eight directions: the four cardinal directions (N, S, E, W) or some combination (NW, NE, SW, SE). Otherwise, it will break.
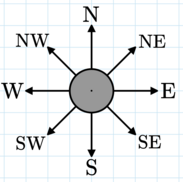 The directions the compass can point.
The directions the compass can point. There are $$$n$$$ distinct points with integer coordinates on a plane. How many ways can you put a compass at one point and the morning star at another so that the compass does not break?
Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \le t \le 10^4$$$). The description of the test cases follows.
The first line of each test case contains a single integer $$$n$$$ ($$$2 \leq n \leq 2 \cdot 10^5$$$) — the number of points.
Then $$$n$$$ lines follow, each line containing two integers $$$x_i$$$, $$$y_i$$$ ($$$-10^9 \leq x_i, y_i \leq 10^9$$$) — the coordinates of each point, all points have distinct coordinates.
It is guaranteed that the sum of $$$n$$$ over all test cases doesn't exceed $$$2 \cdot 10^5$$$.
For each test case, output a single integer — the number of pairs of points that don't break the compass.
530 0-1 -11 144 55 76 910 133-1000000000 10000000000 01000000000 -100000000050 02 2-1 5-1 102 1130 0-1 21 -2
6 2 6 8 0
In the first test case, any pair of points won't break the compass:
- The compass is at $$$(0,0)$$$, the morning star is at $$$(-1,-1)$$$: the compass will point $$$\text{SW}$$$.
- The compass is at $$$(0,0)$$$, the morning star is at $$$(1,1)$$$: the compass will point $$$\text{NE}$$$.
- The compass is at $$$(-1,-1)$$$, the morning star is at $$$(0,0)$$$: the compass will point $$$\text{NE}$$$.
- The compass is at $$$(-1,-1)$$$, the morning star is at $$$(1,1)$$$: the compass will point $$$\text{NE}$$$.
- The compass is at $$$(1,1)$$$, the morning star is at $$$(0,0)$$$: the compass will point $$$\text{SW}$$$.
- The compass is at $$$(1,1)$$$, the morning star is at $$$(-1,-1)$$$: the compass will point $$$\text{SW}$$$.
In the second test case, only two pairs of points won't break the compass:
- The compass is at $$$(6,9)$$$, the morning star is at $$$(10,13)$$$: the compass will point $$$\text{NE}$$$.
- The compass is at $$$(10,13)$$$, the morning star is at $$$(6,9)$$$: the compass will point $$$\text{SW}$$$.
In order to win his toughest battle, Mircea came up with a great strategy for his army. He has $$$n$$$ soldiers and decided to arrange them in a certain way in camps. Each soldier has to belong to exactly one camp, and there is one camp at each integer point on the $$$x$$$-axis (at points $$$\cdots, -2, -1, 0, 1, 2, \cdots$$$).
The strategy consists of $$$m$$$ conditions. Condition $$$i$$$ tells that soldier $$$a_i$$$ should belong to a camp that is situated $$$d_i$$$ meters in front of the camp that person $$$b_i$$$ belongs to. (If $$$d_i < 0$$$, then $$$a_i$$$'s camp should be $$$-d_i$$$ meters behind $$$b_i$$$'s camp.)
Now, Mircea wonders if there exists a partition of soldiers that respects the condition and he asks for your help! Answer "YES" if there is a partition of the $$$n$$$ soldiers that satisfies all of the $$$m$$$ conditions and "NO" otherwise.
Note that two different soldiers may be placed in the same camp.
The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 100$$$) — the number of test cases.
The first line of each test case contains two positive integers $$$n$$$ and $$$m$$$ ($$$2 \leq n \leq 2 \cdot 10^5$$$; $$$1 \leq m \leq n$$$) — the number of soldiers, and the number of conditions respectively.
Then $$$m$$$ lines follow, each of them containing $$$3$$$ integers: $$$a_i$$$, $$$b_i$$$, $$$d_i$$$ ($$$a_i \neq b_i$$$; $$$1 \leq a_i, b_i \leq n$$$; $$$-10^9 \leq d_i \leq 10^9$$$) — denoting the conditions explained in the statement. Note that if $$$d_i$$$ is positive, $$$a_i$$$ should be $$$d_i$$$ meters in front of $$$b_i$$$ and if it is negative, $$$a_i$$$ should be $$$-d_i$$$ meters behind $$$b_i$$$.
Note that the sum of $$$n$$$ over all test cases doesn't exceed $$$2 \cdot 10^5$$$.
For each test case, output "YES" if there is an arrangement of the $$$n$$$ soldiers that satisfies all of the $$$m$$$ conditions and "NO" otherwise.
45 31 2 22 3 44 2 -66 51 2 22 3 44 2 -65 4 43 5 1002 21 2 51 2 44 11 2 3
YES NO NO YES
For the first test case, we can partition the soldiers into camps in the following way: soldier:
- Soldier $$$1$$$ in the camp with the coordinate $$$x = 3$$$.
- Soldier $$$2$$$ in the camp with the coordinate $$$x = 5$$$.
- Soldier $$$3$$$ in the camp with the coordinate $$$x = 9$$$.
- Soldier $$$4$$$ in the camp with the coordinate $$$x = 11$$$.
For the second test case, there is no partition that can satisfy all the constraints at the same time.
For the third test case, there is no partition that satisfies all the constraints since we get contradictory information about the same pair.
For the fourth test case, in order to satisfy the only condition, a possible partition is:
- Soldier $$$1$$$ in the camp with the coordinate $$$x = 10$$$.
- Soldier $$$2$$$ in the camp with the coordinate $$$x = 13$$$.
- Soldier $$$3$$$ in the camp with the coordinate $$$x = -2023$$$.
- Soldier $$$4$$$ in the camp with the coordinate $$$x = -2023$$$.


