You are given a rectangular board of M × N squares. Also you are given an unlimited number of standard domino pieces of 2 × 1 squares. You are allowed to rotate the pieces. You are asked to place as many dominoes as possible on the board so as to meet the following conditions:
1. Each domino completely covers two squares.
2. No two dominoes overlap.
3. Each domino lies entirely inside the board. It is allowed to touch the edges of the board.
Find the maximum number of dominoes, which can be placed under these restrictions.
In a single line you are given two integers M and N — board sizes in squares (1 ≤ M ≤ N ≤ 16).
Output one number — the maximal number of dominoes, which can be placed.
2 4
4
3 3
4
There is a given string S consisting of N symbols. Your task is to find the number of ordered pairs of integers i and j such that
1. 1 ≤ i, j ≤ N
2. S[i] = S[j], that is the i-th symbol of string S is equal to the j-th.
The single input line contains S, consisting of lowercase Latin letters and digits. It is guaranteed that string S in not empty and its length does not exceed 105.
Print a single number which represents the number of pairs i and j with the needed property. Pairs (x, y) and (y, x) should be considered different, i.e. the ordered pairs count.
great10
7
aaaaaaaaaa
100
The Happy Farm 5 creators decided to invent the mechanism of cow grazing. The cows in the game are very slow and they move very slowly, it can even be considered that they stand still. However, carnivores should always be chased off them.
For that a young player Vasya decided to make the shepherd run round the cows along one and the same closed path. It is very important that the cows stayed strictly inside the area limited by the path, as otherwise some cows will sooner or later be eaten. To be absolutely sure in the cows' safety, Vasya wants the path completion time to be minimum.
The new game is launched for different devices, including mobile phones. That's why the developers decided to quit using the arithmetics with the floating decimal point and use only the arithmetics of integers. The cows and the shepherd in the game are represented as points on the plane with integer coordinates. The playing time is modeled by the turns. During every turn the shepherd can either stay where he stands or step in one of eight directions: horizontally, vertically, or diagonally. As the coordinates should always remain integer, then the length of a horizontal and vertical step is equal to 1, and the length of a diagonal step is equal to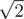 
. The cows do not move. You have to minimize the number of moves the shepherd needs to run round the whole herd.
The first line contains an integer N which represents the number of cows in the herd (1 ≤ N ≤ 105). Each of the next N lines contains two integers Xi and Yi which represent the coordinates of one cow of (|Xi|, |Yi| ≤ 106). Several cows can stand on one point.
Print the single number — the minimum number of moves in the sought path.
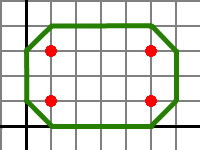
4
1 1
5 1
5 3
1 3
16
Picture for the example test: The coordinate grid is painted grey, the coordinates axes are painted black, the cows are painted red and the sought route is painted green.
The commanding officers decided to drop a nuclear bomb on the enemy's forces. You are ordered to determine the power of the warhead that needs to be used.
The enemy has N strategically important objects. Their positions are known due to the intelligence service. The aim of the strike is to deactivate at least K important objects of the enemy. The bombing impact point is already determined and has coordinates of [X0; Y0].
The nuclear warhead is marked by the estimated impact radius R ≥ 0. All the buildings that are located closer than R to the bombing epicentre will be destroyed. All the buildings that are located further than R from the epicentre, can also be deactivated with some degree of probability. Let's assume that D is the distance between a building and the epicentre. This building's deactivation probability P(D, R) is calculated according to the following formula:
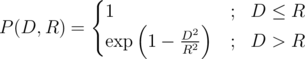
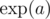as ea, where e ≈ 2.7182818284590452353602874713527If the estimated impact radius of the warhead is equal to zero, then all the buildings located in the impact point will be completely demolished and all the rest of important objects will not be damaged.
The commanding officers want the probability of failing the task to be no more than ε. Nuclear warheads are too expensive a luxury, that's why you have to minimise the estimated impact radius of the warhead.
The first line contains an integer N which represents the number of the enemy's objects (1 ≤ N ≤ 100). The second line contains two integers: K is the required number of deactivated objects, and ε is the maximally permitted probability of not completing the task, given in per mils (1 ≤ K ≤ N, 1 ≤ ε ≤ 999). The third line contains X0 and Y0 which are the coordinates of the strike impact point. The next N lines contain two numbers Xi and Yi each which are the coordinates of every strategically important object. All the coordinates are integer, their absolute values do not exceed 1000.
Let us remind you that there are a thousand per mils in unity (number one).
There can be several objects in one point.
Print the sought estimated impact radius of the warhead. The absolute or relative measure of the inaccuracy of your answer should not exceed 10 - 6.
1
1 500
5 5
1 2
3.84257761518762740
5
3 100
0 0
3 4
60 70
100 100
10 10
5 12
13.45126176453737600
A schoolboy Petya studies square equations. The equations that are included in the school curriculum, usually look simple:
Petya noticed that some equations have two real roots, some of them have only one root and some equations don't have real roots at all. Moreover it turned out that several different square equations can have a common root.
Petya is interested in how many different real roots have all the equations of the type described above for all the possible pairs of numbers b and c such that 1 ≤ b ≤ n, 1 ≤ c ≤ m. Help Petya find that number.
The single line contains two integers n and m. (1 ≤ n, m ≤ 5000000).
Print a single number which is the number of real roots of the described set of equations.
3 3
12
1 2
1
In the second test from the statement the following equations are analysed:
b = 1, c = 1: x2 + 2x + 1 = 0; The root is x = - 1
b = 1, c = 2: x2 + 2x + 2 = 0; No roots
Overall there's one root
In the second test the following equations are analysed:
b = 1, c = 1: x2 + 2x + 1 = 0; The root is x = - 1
b = 1, c = 2: x2 + 2x + 2 = 0; No roots
b = 1, c = 3: x2 + 2x + 3 = 0; No roots
b = 2, c = 1: x2 + 4x + 1 = 0; The roots are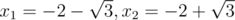 
b = 2, c = 2: x2 + 4x + 2 = 0; The roots are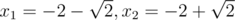 
b = 2, c = 3: x2 + 4x + 3 = 0; The roots are x1 = - 3, x2 = - 1
b = 3, c = 1: x2 + 6x + 1 = 0; The roots are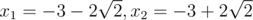 
b = 3, c = 2: x2 + 6x + 2 = 0; The roots are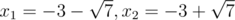 
b = 3, c = 3: x2 + 6x + 3 = 0; The roots are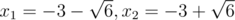 
Overall there are 13 roots and as the root - 1 is repeated twice, that means there are 12 different roots.