Bear Limak wants to become the largest of bears, or at least to become larger than his brother Bob.
Right now, Limak and Bob weigh a and b respectively. It's guaranteed that Limak's weight is smaller than or equal to his brother's weight.
Limak eats a lot and his weight is tripled after every year, while Bob's weight is doubled after every year.
After how many full years will Limak become strictly larger (strictly heavier) than Bob?
The only line of the input contains two integers a and b (1 ≤ a ≤ b ≤ 10) — the weight of Limak and the weight of Bob respectively.
Print one integer, denoting the integer number of years after which Limak will become strictly larger than Bob.
4 7
2
4 9
3
1 1
1
In the first sample, Limak weighs 4 and Bob weighs 7 initially. After one year their weights are 4·3 = 12 and 7·2 = 14 respectively (one weight is tripled while the other one is doubled). Limak isn't larger than Bob yet. After the second year weights are 36 and 28, so the first weight is greater than the second one. Limak became larger than Bob after two years so you should print 2.
In the second sample, Limak's and Bob's weights in next years are: 12 and 18, then 36 and 36, and finally 108 and 72 (after three years). The answer is 3. Remember that Limak wants to be larger than Bob and he won't be satisfied with equal weights.
In the third sample, Limak becomes larger than Bob after the first year. Their weights will be 3 and 2 then.
Bear Limak examines a social network. Its main functionality is that two members can become friends (then they can talk with each other and share funny pictures).
There are n members, numbered 1 through n. m pairs of members are friends. Of course, a member can't be a friend with themselves.
Let A-B denote that members A and B are friends. Limak thinks that a network is reasonable if and only if the following condition is satisfied: For every three distinct members (X, Y, Z), if X-Y and Y-Z then also X-Z.
For example: if Alan and Bob are friends, and Bob and Ciri are friends, then Alan and Ciri should be friends as well.
Can you help Limak and check if the network is reasonable? Print "YES" or "NO" accordingly, without the quotes.
The first line of the input contain two integers n and m (3 ≤ n ≤ 150 000, 
) — the number of members and the number of pairs of members that are friends.
The i-th of the next m lines contains two distinct integers ai and bi (1 ≤ ai, bi ≤ n, ai ≠ bi). Members ai and bi are friends with each other. No pair of members will appear more than once in the input.
If the given network is reasonable, print "YES" in a single line (without the quotes). Otherwise, print "NO" in a single line (without the quotes).
4 3
1 3
3 4
1 4
YES
4 4
3 1
2 3
3 4
1 2
NO
10 4
4 3
5 10
8 9
1 2
YES
3 2
1 2
2 3
NO
The drawings below show the situation in the first sample (on the left) and in the second sample (on the right). Each edge represents two members that are friends. The answer is "NO" in the second sample because members (2, 3) are friends and members (3, 4) are friends, while members (2, 4) are not.
In the army, it isn't easy to form a group of soldiers that will be effective on the battlefield. The communication is crucial and thus no two soldiers should share a name (what would happen if they got an order that Bob is a scouter, if there are two Bobs?).
A group of soldiers is effective if and only if their names are different. For example, a group (John, Bob, Limak) would be effective, while groups (Gary, Bob, Gary) and (Alice, Alice) wouldn't.
You are a spy in the enemy's camp. You noticed n soldiers standing in a row, numbered 1 through n. The general wants to choose a group of k consecutive soldiers. For every k consecutive soldiers, the general wrote down whether they would be an effective group or not.
You managed to steal the general's notes, with n - k + 1 strings s1, s2, ..., sn - k + 1, each either "YES" or "NO".
- The string s1 describes a group of soldiers 1 through k ("YES" if the group is effective, and "NO" otherwise).
- The string s2 describes a group of soldiers 2 through k + 1.
- And so on, till the string sn - k + 1 that describes a group of soldiers n - k + 1 through n.
Your task is to find possible names of n soldiers. Names should match the stolen notes. Each name should be a string that consists of between 1 and 10 English letters, inclusive. The first letter should be uppercase, and all other letters should be lowercase. Names don't have to be existing names — it's allowed to print "Xyzzzdj" or "T" for example.
Find and print any solution. It can be proved that there always exists at least one solution.
The first line of the input contains two integers n and k (2 ≤ k ≤ n ≤ 50) — the number of soldiers and the size of a group respectively.
The second line contains n - k + 1 strings s1, s2, ..., sn - k + 1. The string si is "YES" if the group of soldiers i through i + k - 1 is effective, and "NO" otherwise.
Find any solution satisfying all given conditions. In one line print n space-separated strings, denoting possible names of soldiers in the order. The first letter of each name should be uppercase, while the other letters should be lowercase. Each name should contain English letters only and has length from 1 to 10.
If there are multiple valid solutions, print any of them.
8 3
NO NO YES YES YES NO
Adam Bob Bob Cpqepqwer Limak Adam Bob Adam
9 8
YES NO
R Q Ccccccccc Ccocc Ccc So Strong Samples Ccc
3 2
NO NO
Na Na Na
In the first sample, there are 8 soldiers. For every 3 consecutive ones we know whether they would be an effective group. Let's analyze the provided sample output:
- First three soldiers (i.e. Adam, Bob, Bob) wouldn't be an effective group because there are two Bobs. Indeed, the string s1 is "NO".
- Soldiers 2 through 4 (Bob, Bob, Cpqepqwer) wouldn't be effective either, and the string s2 is "NO".
- Soldiers 3 through 5 (Bob, Cpqepqwer, Limak) would be effective, and the string s3 is "YES".
- ...,
- Soldiers 6 through 8 (Adam, Bob, Adam) wouldn't be effective, and the string s6 is "NO".
A tree is an undirected connected graph without cycles. The distance between two vertices is the number of edges in a simple path between them.
Limak is a little polar bear. He lives in a tree that consists of n vertices, numbered 1 through n.
Limak recently learned how to jump. He can jump from a vertex to any vertex within distance at most k.
For a pair of vertices (s, t) we define f(s, t) as the minimum number of jumps Limak needs to get from s to t. Your task is to find the sum of f(s, t) over all pairs of vertices (s, t) such that s < t.
The first line of the input contains two integers n and k (2 ≤ n ≤ 200 000, 1 ≤ k ≤ 5) — the number of vertices in the tree and the maximum allowed jump distance respectively.
The next n - 1 lines describe edges in the tree. The i-th of those lines contains two integers ai and bi (1 ≤ ai, bi ≤ n) — the indices on vertices connected with i-th edge.
It's guaranteed that the given edges form a tree.
Print one integer, denoting the sum of f(s, t) over all pairs of vertices (s, t) such that s < t.
6 2
1 2
1 3
2 4
2 5
4 6
20
13 3
1 2
3 2
4 2
5 2
3 6
10 6
6 7
6 13
5 8
5 9
9 11
11 12
114
3 5
2 1
3 1
3
In the first sample, the given tree has 6 vertices and it's displayed on the drawing below. Limak can jump to any vertex within distance at most 2. For example, from the vertex 5 he can jump to any of vertices: 1, 2 and 4 (well, he can also jump to the vertex 5 itself).
There are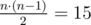 
pairs of vertices (s, t) such that s < t. For 5 of those pairs Limak would need two jumps: (1, 6), (3, 4), (3, 5), (3, 6), (5, 6). For other 10 pairs one jump is enough. So, the answer is 5·2 + 10·1 = 20.
In the third sample, Limak can jump between every two vertices directly. There are 3 pairs of vertices (s < t), so the answer is 3·1 = 3.
Bear Limak prepares problems for a programming competition. Of course, it would be unprofessional to mention the sponsor name in the statement. Limak takes it seriously and he is going to change some words. To make it still possible to read, he will try to modify each word as little as possible.
Limak has a string s that consists of uppercase English letters. In one move he can swap two adjacent letters of the string. For example, he can transform a string "ABBC" into "BABC" or "ABCB" in one move.
Limak wants to obtain a string without a substring "VK" (i.e. there should be no letter 'V' immediately followed by letter 'K'). It can be easily proved that it's possible for any initial string s.
What is the minimum possible number of moves Limak can do?
The first line of the input contains an integer n (1 ≤ n ≤ 75) — the length of the string.
The second line contains a string s, consisting of uppercase English letters. The length of the string is equal to n.
Print one integer, denoting the minimum possible number of moves Limak can do, in order to obtain a string without a substring "VK".
4
VKVK
3
5
BVVKV
2
7
VVKEVKK
3
20
VKVKVVVKVOVKVQKKKVVK
8
5
LIMAK
0
In the first sample, the initial string is "VKVK". The minimum possible number of moves is 3. One optimal sequence of moves is:
- Swap two last letters. The string becomes "VKKV".
- Swap first two letters. The string becomes "KVKV".
- Swap the second and the third letter. The string becomes "KKVV". Indeed, this string doesn't have a substring "VK".
In the second sample, there are two optimal sequences of moves. One is "BVVKV" → "VBVKV" → "VVBKV". The other is "BVVKV" → "BVKVV" → "BKVVV".
In the fifth sample, no swaps are necessary.