Codeforces Round 871 (Div. 4)
A. Love Story
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output

Timur loves codeforces. That's why he has a string $$$s$$$ having length $$$10$$$ made containing only lowercase Latin letters. Timur wants to know how many indices string $$$s$$$ differs from the string "codeforces".

For example string $$$s =$$$ "coolforsez" differs from "codeforces" in $$$4$$$ indices, shown in bold.

Help Timur by finding the number of indices where string $$$s$$$ differs from "codeforces".

Note that you can't reorder the characters in the string $$$s$$$.

Input

The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 1000$$$) — the number of test cases.

Each test case is one line and contains the string $$$s$$$, consisting of exactly $$$10$$$ lowercase Latin characters.

Output

For each test case, output a single integer — the number of indices where string $$$s$$$ differs.

Example
Input
5
coolforsez
cadafurcie
codeforces
paiuforces
forcescode
Output
4
5
0
4
9

B. Blank Space
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output

You are given a binary array $$$a$$$ of $$$n$$$ elements, a binary array is an array consisting only of $$$0$$$s and $$$1$$$s.

A blank space is a segment of consecutive elements consisting of only $$$0$$$s.

Your task is to find the length of the longest blank space.

Input

The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 1000$$$) — the number of test cases.

The first line of each test case contains a single integer $$$n$$$ ($$$1 \leq n \leq 100$$$) — the length of the array.

The second line of each test case contains $$$n$$$ space-separated integers $$$a_i$$$ ($$$0 \leq a_i \leq 1$$$) — the elements of the array.

Output

For each test case, output a single integer — the length of the longest blank space.

Example
Input
5
5
1 0 0 1 0
4
0 1 1 1
1
0
3
1 1 1
9
1 0 0 0 1 0 0 0 1
Output
2
1
1
0
3

C. Mr. Perfectly Fine
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

Victor wants to become "Mr. Perfectly Fine". For that, he needs to acquire a certain set of skills. More precisely, he has $$$2$$$ skills he needs to acquire.

Victor has $$$n$$$ books. Reading book $$$i$$$ takes him $$$m_i$$$ minutes and will give him some (possibly none) of the required two skills, represented by a binary string of length $$$2$$$.

What is the minimum amount of time required so that Victor acquires all of the two skills?

Input

The input consists of multiple test cases. The first line contains an integer $$$t$$$ ($$$1 \leq t \leq 1000$$$) — the number of test cases. The description of the test cases follows.

The first line of each test case contains an integer $$$n$$$ ($$$1 \leq n \leq 2 \cdot 10^5$$$) — the number of books available.

Then $$$n$$$ lines follow. Line $$$i$$$ contains a positive integer $$$m_i$$$ ($$$1 \leq m_i \leq 2 \cdot 10^5$$$) and a binary string of length $$$2$$$, where $$$s_{i1} = 1$$$ if reading book $$$i$$$ acquires Victor skill $$$1$$$, and $$$s_{i1} = 0$$$ otherwise, and $$$s_{i2} = 1$$$ if reading book $$$i$$$ acquires Victor skill $$$2$$$, and $$$s_{i2} = 0$$$ otherwise.

It is guaranteed that the sum of $$$n$$$ over all test cases doesn't exceed $$$2 \cdot 10^5$$$.

Output

For each test case, output a single integer denoting the minimum amount of minutes required for Victor to obtain both needed skills and $$$-1$$$ in case it's impossible to obtain the two skills after reading any amount of books.

Example
Input
6
4
2 00
3 10
4 01
4 00
5
3 01
3 01
5 01
2 10
9 10
1
5 11
3
9 11
8 01
7 10
6
4 01
6 01
7 01
8 00
9 01
1 00
4
8 00
9 10
9 11
8 11
Output
7
5
5
9
-1
8
Note

In the first test case, we can use books $$$2$$$ and $$$3$$$, with a total amount of minutes spent equal to $$$3 + 4 = 7$$$.

In the second test case, we can use the books $$$1$$$ and $$$4$$$, with a total amount of minutes spent equal to $$$3 + 2 = 5$$$.

In the third test case, we have only one option and that is reading book $$$1$$$ for a total amount of minutes spent equal to $$$5$$$.

D. Gold Rush
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

Initially you have a single pile with $$$n$$$ gold nuggets. In an operation you can do the following:

  • Take any pile and split it into two piles, so that one of the resulting piles has exactly twice as many gold nuggets as the other. (All piles should have an integer number of nuggets.)

One possible move is to take a pile of size $$$6$$$ and split it into piles of sizes $$$2$$$ and $$$4$$$, which is valid since $$$4$$$ is twice as large as $$$2$$$.

Can you make a pile with exactly $$$m$$$ gold nuggets using zero or more operations?
Input

The first line contains an integer $$$t$$$ ($$$1 \leq t \leq 1000$$$) — the number of test cases.

The only line of each test case contains two integers $$$n$$$ and $$$m$$$ ($$$1 \leq n, m \leq 10^7$$$) — the starting and target pile sizes, respectively.

Output

For each test case, output "YES" if you can make a pile of size exactly $$$m$$$, and "NO" otherwise.

You can output the answer in any case (for example, the strings "yEs", "yes", "Yes" and "YES" will be recognized as a positive answer).

Example
Input
11
6 4
9 4
4 2
18 27
27 4
27 2
27 10
1 1
3 1
5 1
746001 2984004
Output
YES
YES
NO
NO
YES
YES
NO
YES
YES
NO
NO
Note

The first test case is pictured in the statement. We can make a pile of size $$$4$$$.

In the second test case, we can perform the following operations: $$$\{\color{red}{9}\} \to \{\color{red}{6},3\} \to \{4,2,3\}$$$. The pile that is split apart is colored red before each operation.

In the third test case, we can't perform a single operation.

In the fourth test case, we can't end up with a larger pile than we started with.

E. The Lakes
time limit per test
3 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

You are given an $$$n \times m$$$ grid $$$a$$$ of non-negative integers. The value $$$a_{i,j}$$$ represents the depth of water at the $$$i$$$-th row and $$$j$$$-th column.

A lake is a set of cells such that:

  • each cell in the set has $$$a_{i,j} > 0$$$, and
  • there exists a path between any pair of cells in the lake by going up, down, left, or right a number of times and without stepping on a cell with $$$a_{i,j} = 0$$$.

The volume of a lake is the sum of depths of all the cells in the lake.

Find the largest volume of a lake in the grid.

Input

The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — the number of test cases.

The first line of each test case contains two integers $$$n, m$$$ ($$$1 \leq n, m \leq 1000$$$) — the number of rows and columns of the grid, respectively.

Then $$$n$$$ lines follow each with $$$m$$$ integers $$$a_{i,j}$$$ ($$$0 \leq a_{i,j} \leq 1000$$$) — the depth of the water at each cell.

It is guaranteed that the sum of $$$n \cdot m$$$ over all test cases does not exceed $$$10^6$$$.

Output

For each test case, output a single integer — the largest volume of a lake in the grid.

Example
Input
5
3 3
1 2 0
3 4 0
0 0 5
1 1
0
3 3
0 1 1
1 0 1
1 1 1
5 5
1 1 1 1 1
1 0 0 0 1
1 0 5 0 1
1 0 0 0 1
1 1 1 1 1
5 5
1 1 1 1 1
1 0 0 0 1
1 1 4 0 1
1 0 0 0 1
1 1 1 1 1
Output
10
0
7
16
21

F. Forever Winter
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

A snowflake graph is generated from two integers $$$x$$$ and $$$y$$$, both greater than $$$1$$$, as follows:

  • Start with one central vertex.
  • Connect $$$x$$$ new vertices to this central vertex.
  • Connect $$$y$$$ new vertices to each of these $$$x$$$ vertices.
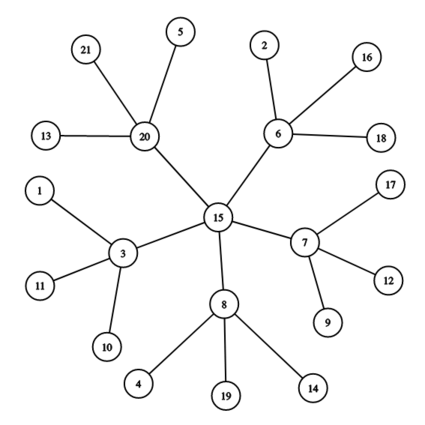
For example, below is a snowflake graph for $$$x=5$$$ and $$$y=3$$$.

The snowflake graph above has a central vertex $$$15$$$, then $$$x=5$$$ vertices attached to it ($$$3$$$, $$$6$$$, $$$7$$$, $$$8$$$, and $$$20$$$), and then $$$y=3$$$ vertices attached to each of those.

Given a snowflake graph, determine the values of $$$x$$$ and $$$y$$$.
Input

The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 1000$$$) — the number of test cases.

The first line of each test case contains two integers $$$n$$$ and $$$m$$$ ($$$2 \leq n \leq 200$$$; $$$1 \leq m \leq \min\left(1000, \frac{n(n-1)}{2}\right)$$$) — the number of vertices and edges in the graph, respectively.

The next $$$m$$$ lines each contain two integers each $$$u$$$ and $$$v$$$ ($$$1 \leq u, v \leq n$$$, $$$u \neq v$$$) — the numbers of vertices connected by an edge. The graph does not contain multiple edges and self-loops.

It is guaranteed that this graph is a snowflake graph for some integers $$$x$$$ and $$$y$$$ both greater than $$$1$$$.

Output

For each test case, on a separate line output the values of $$$x$$$ and $$$y$$$, in that order, separated by a space.

Example
Input
3
21 20
21 20
5 20
13 20
1 3
11 3
10 3
4 8
19 8
14 8
9 7
12 7
17 7
18 6
16 6
2 6
6 15
7 15
8 15
20 15
3 15
7 6
1 2
1 3
2 4
2 5
3 6
3 7
9 8
9 3
3 6
6 2
2 1
5 2
2 7
4 3
3 8
Output
5 3
2 2
2 3
Note

The first test case is pictured in the statement. Note that the output 3 5 is incorrect, since $$$x$$$ should be output before $$$y$$$.

G. Hits Different
time limit per test
2.5 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

In a carnival game, there is a huge pyramid of cans with $$$2023$$$ rows, numbered in a regular pattern as shown.

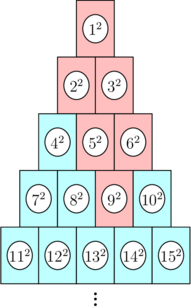
If can $$$9^2$$$ is hit initially, then all cans colored red in the picture above would fall.

You throw a ball at the pyramid, and it hits a single can with number $$$n^2$$$. This causes all cans that are stacked on top of this can to fall (that is, can $$$n^2$$$ falls, then the cans directly above $$$n^2$$$ fall, then the cans directly above those cans, and so on). For example, the picture above shows the cans that would fall if can $$$9^2$$$ is hit.

What is the sum of the numbers on all cans that fall? Recall that $$$n^2 = n \times n$$$.

Input

The first line contains an integer $$$t$$$ ($$$1 \leq t \leq 1000$$$) — the number of test cases.

The only line of each test case contains a single integer $$$n$$$ ($$$1 \leq n \leq 10^6$$$) — it means that the can you hit has label $$$n^2$$$.

Output

For each test case, output a single integer — the sum of the numbers on all cans that fall.

Please note, that the answer for some test cases won't fit into 32-bit integer type, so you should use at least 64-bit integer type in your programming language (like long long for C++). For all valid inputs, the answer will always fit into 64-bit integer type.

Example
Input
10
9
1
2
3
4
5
6
10
1434
1000000
Output
156
1
5
10
21
39
46
146
63145186
58116199242129511
Note

The first test case is pictured in the statement. The sum of the numbers that fall is $$$$$$1^2 + 2^2 + 3^2 + 5^2 + 6^2 + 9^2 = 1 + 4 + 9 + 25 + 36 + 81 = 156.$$$$$$

In the second test case, only the can labeled $$$1^2$$$ falls, so the answer is $$$1^2=1$$$.

In the third test case, the cans labeled $$$1^2$$$ and $$$2^2$$$ fall, so the answer is $$$1^2+2^2=1+4=5$$$.

In the fourth test case, the cans labeled $$$1^2$$$ and $$$3^2$$$ fall, so the answer is $$$1^2+3^2=1+9=10$$$.

In the fifth test case, the cans labeled $$$1^2$$$, $$$2^2$$$, and $$$4^2$$$ fall, so the answer is $$$1^2+2^2+4^2=1+4+16=21$$$.

H. Don't Blame Me
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

Sadly, the problem setter couldn't think of an interesting story, thus he just asks you to solve the following problem.

Given an array $$$a$$$ consisting of $$$n$$$ positive integers, count the number of non-empty subsequences for which the bitwise $$$\mathsf{AND}$$$ of the elements in the subsequence has exactly $$$k$$$ set bits in its binary representation. The answer may be large, so output it modulo $$$10^9+7$$$.

Recall that the subsequence of an array $$$a$$$ is a sequence that can be obtained from $$$a$$$ by removing some (possibly, zero) elements. For example, $$$[1, 2, 3]$$$, $$$[3]$$$, $$$[1, 3]$$$ are subsequences of $$$[1, 2, 3]$$$, but $$$[3, 2]$$$ and $$$[4, 5, 6]$$$ are not.

Note that $$$\mathsf{AND}$$$ represents the bitwise AND operation.

Input

Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \le t \le 10^4$$$). The description of the test cases follows.

The first line of each test case consists of two integers $$$n$$$ and $$$k$$$ ($$$1 \leq n \leq 2 \cdot 10^5$$$, $$$0 \le k \le 6$$$) — the length of the array and the number of set bits that the bitwise $$$\mathsf{AND}$$$ the counted subsequences should have in their binary representation.

The second line of each test case consists of $$$n$$$ integers $$$a_i$$$ ($$$0 \leq a_i \leq 63$$$) — the array $$$a$$$.

It is guaranteed that the sum of $$$n$$$ over all test cases doesn't exceed $$$2 \cdot 10^5$$$.

Output

For each test case, output a single integer — the number of subsequences that have exactly $$$k$$$ set bits in their bitwise $$$\mathsf{AND}$$$ value's binary representation. The answer may be large, so output it modulo $$$10^9+7$$$.

Example
Input
6
5 1
1 1 1 1 1
4 0
0 1 2 3
5 1
5 5 7 4 2
1 2
3
12 0
0 2 0 2 0 2 0 2 0 2 0 2
10 6
63 0 63 5 5 63 63 4 12 13
Output
31
10
10
1
4032
15